题目内容
曲线 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )
轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )A.

B.

C.π
D.2π
【答案】分析:利用两角和与差的三角函数化简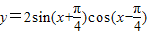 ,然后求出曲线与y=
,然后求出曲线与y= 的y轴右侧的交点按横坐标,即可求出|P2P4|.
的y轴右侧的交点按横坐标,即可求出|P2P4|.
解答:解: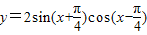 =
= (sinx+cosx)
(sinx+cosx)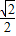 (cosx+sinx)=1+sin2x;它与y=
(cosx+sinx)=1+sin2x;它与y= 的交点,就是sin2x=-
的交点,就是sin2x=- 的根,解得2x=
的根,解得2x= ;
;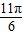 ;
;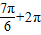 ;
;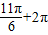 ;…
;…
所以x=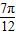 ;
;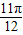 ,
,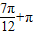 ,
, …,所以|P2P4|=
…,所以|P2P4|=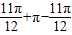 =π;
=π;
故选C
点评:本题是基础题,考查三角函数的化简求值,方程的根就是函数图象的交点,考查计算能力,可以利用周期解答本题.
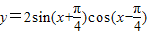 ,然后求出曲线与y=
,然后求出曲线与y= 的y轴右侧的交点按横坐标,即可求出|P2P4|.
的y轴右侧的交点按横坐标,即可求出|P2P4|.解答:解:
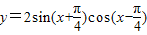 =
= (sinx+cosx)
(sinx+cosx)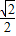 (cosx+sinx)=1+sin2x;它与y=
(cosx+sinx)=1+sin2x;它与y= 的交点,就是sin2x=-
的交点,就是sin2x=- 的根,解得2x=
的根,解得2x= ;
;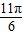 ;
;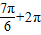 ;
;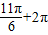 ;…
;…所以x=
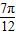 ;
;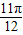 ,
,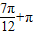 ,
, …,所以|P2P4|=
…,所以|P2P4|=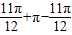 =π;
=π;故选C
点评:本题是基础题,考查三角函数的化简求值,方程的根就是函数图象的交点,考查计算能力,可以利用周期解答本题.

练习册系列答案
相关题目
 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )
轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )

 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )
轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )

 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )
轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )

 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )
轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于( )
