题目内容
已知正三角形ABC边长为a,用这个三角形的高为边,作一个新的正三角形,再用这第二个正三角形的高为边作正三角形,…,这样无限继续下去,则所有正三角形的面积之和为 .
【答案】分析:先设第n个三角形的面积为an,根据三角形面积公式得出a1,a2,a3,发现数列{an}为等比数列,进而求出前n项和的极限,即可得到答案.
解答:解:设第n个三角形的面积为an,则a1= ×a×a×sin60°=
×a×a×sin60°=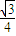 a2,
a2,
a2= ×
× a×
a×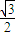 a×sin60°=
a×sin60°=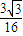 a2=
a2= ×
×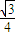 a2,
a2,
a3= ×
× a×
a× a×sin60°=
a×sin60°=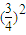 ×
× a2;
a2;
…
∴数列{an}为首项为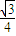 a2,公比为
a2,公比为  的等比数列.
的等比数列.
所有这些三角形的面积的和为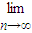 (a1+a2+…+an)=
(a1+a2+…+an)=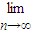
 =
=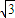 a2.
a2.
故答案为: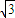 a2.
a2.
点评:本题主要考查了等比数列的应用以及相似三角形的性质,相似三角形面积的比等于相似比的平方.
解答:解:设第n个三角形的面积为an,则a1=
 ×a×a×sin60°=
×a×a×sin60°=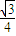 a2,
a2,a2=
 ×
× a×
a×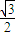 a×sin60°=
a×sin60°=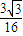 a2=
a2= ×
×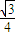 a2,
a2,a3=
 ×
× a×
a× a×sin60°=
a×sin60°=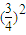 ×
× a2;
a2;…
∴数列{an}为首项为
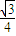 a2,公比为
a2,公比为  的等比数列.
的等比数列.所有这些三角形的面积的和为
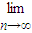 (a1+a2+…+an)=
(a1+a2+…+an)=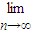
 =
=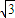 a2.
a2.故答案为:
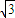 a2.
a2.点评:本题主要考查了等比数列的应用以及相似三角形的性质,相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
 如图,已知正三角形ABC的边长为2,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则
如图,已知正三角形ABC的边长为2,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则 最小,并求出最小值.
最小,并求出最小值.