题目内容
设集合p={x|2x2-5x-12≤0},Q={x|(x-2a)(a-x)>0},若P∩Q=∅,则实数a的取值范围 .
考点:交集及其运算
专题:集合
分析:当a>0时,Q={x|a<x<2a},由P∩Q=∅,得a>4;当a=0时,Q=∅,P∩Q=∅成立;当a<0时,Q={x|2a<x<a},
由P∩Q=∅,得a<-
.由此能求出实数a的取值范围.
由P∩Q=∅,得a<-
| 3 |
| 2 |
解答:
解:∵p={x|2x2-5x-12≤0}={x|-
≤x≤4},
Q={x|(x-2a)(a-x)>0},
∴当a>0时,Q={x|a<x<2a},
由P∩Q=∅,得a>4;
当a=0时,Q=∅,P∩Q=∅成立;
当a<0时,Q={x|2a<x<a},
由P∩Q=∅,得a<-
.
综上所述,实数a的取值范围是{-∞,-
}∪{0}∪{4,+∞}.
故答案为:{-∞,-
}∪{0}∪{4,+∞}.
| 3 |
| 2 |
Q={x|(x-2a)(a-x)>0},
∴当a>0时,Q={x|a<x<2a},
由P∩Q=∅,得a>4;
当a=0时,Q=∅,P∩Q=∅成立;
当a<0时,Q={x|2a<x<a},
由P∩Q=∅,得a<-
| 3 |
| 2 |
综上所述,实数a的取值范围是{-∞,-
| 3 |
| 2 |
故答案为:{-∞,-
| 3 |
| 2 |
点评:本题考查实数的取值范围的求法,是基础题,解题时要注意分类讨论思想和交集性质的合理运用.

练习册系列答案
相关题目
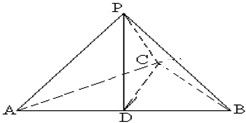 如图,已知三棱锥P-ABC,D为AB的中点,且△PDB是正三角形,PA⊥PC.求证:PC⊥BC.
如图,已知三棱锥P-ABC,D为AB的中点,且△PDB是正三角形,PA⊥PC.求证:PC⊥BC.