题目内容
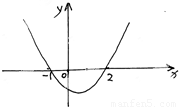
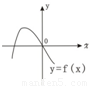
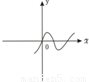
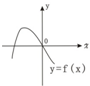 如图所示为二次函数f(x)的图象,若函数g(x)=f'(x)f(x),(f'(x)是f(x)的导函数),则g(x)的图象是( )
如图所示为二次函数f(x)的图象,若函数g(x)=f'(x)f(x),(f'(x)是f(x)的导函数),则g(x)的图象是( )分析:由题意可得f'(x)的图象首先应该在x轴的上方,再变化到x轴的下方,所以得到函数g(x)=f'(x)f(x)的图象开始时应该在x轴的下方,当x>0时,f'(x)<0,f(x)<0,可得当x>0时,函数g(x)=f'(x)f(x)的图象在x轴上方.
解答:解:由二次函数f(x)的图象可得f'(x)的图象首先应该在x轴的上方,再变化到x轴的下方,
所以函数g(x)=f'(x)f(x)的图象开始时应该在x轴的下方,
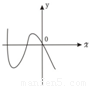
所以排除B、D两个答案.
又因为当x>0时,f'(x)<0,f(x)<0,
所以当x>0时,函数g(x)=f'(x)f(x)的图象在x轴的上方.
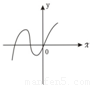
故选A.
所以函数g(x)=f'(x)f(x)的图象开始时应该在x轴的下方,
所以排除B、D两个答案.
又因为当x>0时,f'(x)<0,f(x)<0,
所以当x>0时,函数g(x)=f'(x)f(x)的图象在x轴的上方.
故选A.
点评:解决此类问题的关键是熟练掌握函数的单调性与函数导数之间的关系,此题属于基础题,在观察图象时小心仔细即可得到全分.

练习册系列答案
相关题目
 如图所示为二次函数f(x)的图象,已知-1<x1<x2<2,那么(x1+1)f(x2)-(x2+1)f(x1)为( )
如图所示为二次函数f(x)的图象,已知-1<x1<x2<2,那么(x1+1)f(x2)-(x2+1)f(x1)为( )