题目内容
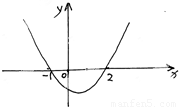
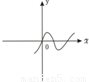
如图所示为二次函数f（x）的图象，已知-1＜x1＜x2＜2，那么（x1+1）f（x2）-（x2+1）f（x1）为（ ）分析：由图设f（x）=a（x+1）（x-2）且a＞0，求出f（x1）和f（x2），代入（x1+1）﹒f（x2）-（x2+1）﹒f（x1）化简，再由已知的范围判断出各个因式的符号即可．
解答：解：由图设f（x）=a（x+1）（x-2），（a＞0）
则f（x1）=a（x1+1）（x1-2），f（x2）=a（x2+1）（x2-2），
∴（x1+1）﹒f（x2）-（x2+1）﹒f（x1）
=（x1+1）﹒a（x2+1）（x2-2）-（x2+1）﹒a（x1+1）（x1-2）
=a（x1+1）（x2+1）[（x2-2）-（x1-2）]
=a（x1+1）（x2+1）（x2-x1）
∵-1＜x1＜x2＜2，∴x1+1＞0，x2+1＞0，x2-x1＞0，
又a＞0，则a（x1+1）（x2+1）（x2-x1）＞0，
∴（x1+1）﹒f（x2）-（x2+1）﹒f（x1）＞0，
故选A．
则f（x1）=a（x1+1）（x1-2），f（x2）=a（x2+1）（x2-2），
∴（x1+1）﹒f（x2）-（x2+1）﹒f（x1）
=（x1+1）﹒a（x2+1）（x2-2）-（x2+1）﹒a（x1+1）（x1-2）
=a（x1+1）（x2+1）[（x2-2）-（x1-2）]
=a（x1+1）（x2+1）（x2-x1）
∵-1＜x1＜x2＜2，∴x1+1＞0，x2+1＞0，x2-x1＞0，
又a＞0，则a（x1+1）（x2+1）（x2-x1）＞0，
∴（x1+1）﹒f（x2）-（x2+1）﹒f（x1）＞0，
故选A．
点评：本题考查了二次函数解析式的两根式，以及式子的化简，判断符号等，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
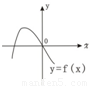
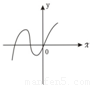
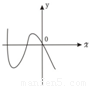
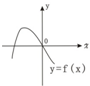如图所示为二次函数f（x）的图象，若函数g（x）=f'（x）f（x），（f'（x）是f（x）的导函数），则g（x）的图象是（ ）
