题目内容
圆C的方程为（x-2）2+y2=4，圆M的方程为（x-2-5sinθ）2+（y-5cosθ）2=1（θ∈R），过圆C上任意一点P作圆M的两条切线PE、PF，切点分别为E、F，则
•
的最小值是（ ）
| PE |
| PF |
| A、6 | ||
B、
| ||
| C、7 | ||
D、
|
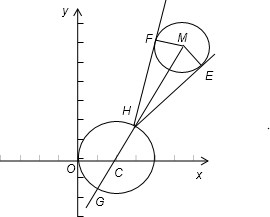
分析：由两圆的圆心距|CM|=5大于两圆的半径之和可得两圆相离，如图所示，则
•
的最小值是
•
，
利用 两个向量的数量积的定义求出
•
的值，即为所求．
| PE |
| PF |
| HE |
| HF |
利用 两个向量的数量积的定义求出
| HE |
| HF |
解答：解：（x-2）2+y2=4的圆心C（2，0），半径等于2，圆M （x-2-5sinθ）2+（y-5cosθ）2=1，
圆心M（2+5sinθ，5cosθ），半径等于1．∵|CM|=
=5＞2+1，故两圆相离．
∵
•
=|
|•
•cos∠EPF，要使
•
最小，需|
| 和
最小，且∠EPF 最大，
如图所示，设直线CM 和圆C 交于H、G两点，则
•
的最小值是
•
．
|H M|=|CM|-2=5-2=3，|H E|=
=
=2
，sin∠MHE=
=
，
∴cos∠EHF=cos2∠MHE=1-2sin2∠MHE=
，
∴
•
=|H E|•|H E|•cos∠EHF=2
×2
×
=
，故选 B．
圆心M（2+5sinθ，5cosθ），半径等于1．∵|CM|=
| (5sinθ)2+(5cosθ)2 |
∵
| PE |
| PF |
| PE |
| |PF| |
| PE |
| PF |
| PE |
| |PF| |
如图所示，设直线CM 和圆C 交于H、G两点，则
| PE |
| PF |
| HE |
| HF |
|H M|=|CM|-2=5-2=3，|H E|=
| |HM|2-|ME|2 |
| 9-1 |
| 2 |
| |ME| |
| |MH| |
| 1 |
| 3 |
∴cos∠EHF=cos2∠MHE=1-2sin2∠MHE=
| 7 |
| 9 |
∴
| HE |
| HF |
| 2 |
| 2 |
| 7 |
| 9 |
| 56 |
| 9 |
点评：本题考查两圆的位置关系，两圆的切线，两个向量的数量积的定义，二倍角的余弦公式，体现了数形结合
的数学思想，判断
•
的最小值是
•
，是解题的关键，属于中档题．
的数学思想，判断
| PE |
| PF |
| HE |
| HF |
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目