题目内容
设函数f (x)的定义域为M,具有性质P:对任意x∈M,都有f (x)+f (x+2)≤2f (x+1).
(1)若M为实数集R,是否存在函数f (x)=ax (a>0且a≠1,x∈R) 具有性质P,并说明理由;
(2)若M为自然数集N,并满足对任意x∈M,都有f (x)∈N. 记d(x)=f (x+1)-f (x).
(ⅰ) 求证:对任意x∈M,都有d(x+1)≤d(x)且d(x)≥0;
(ⅱ) 求证:存在整数0≤c≤d(1)及无穷多个正整数n,满足d(n)=c.
(1)根据新定义可知,不存在函数f (x)=ax(a>0且a≠1)满足性质P.
(2)运用反证法来证明正难则反的试题。也是证明不等式常用的方法之一。
【解析】
试题分析:证明:(1)因f (x)=ax(a>0且a≠1),所以ax≠ax+2,即f (x)≠f (x+2).
2分
由题设以及算术平均与几何平均不等式,得
f
(x)+f (x+2)=ax+ax+2>2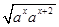 =2 ax+1=2 f (x+1),
=2 ax+1=2 f (x+1),
这与f (x)+f (x+2)≤2f (x+1)矛盾.
故不存在函数f (x)=ax(a>0且a≠1)满足性质P. 4分
(2)(ⅰ)由题设对任意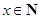 ,f (x)+f (x+2)≤2f
(x+1),所以
,f (x)+f (x+2)≤2f
(x+1),所以
f(x+2)-f(x+1)≤f(x+1)-f(x).
于是对任意x∈N,d(x+1)≤d(x). 6分
下面用反证法证明:对任意x∈N,d(x)≥0.
假设存在某个非负整数k使d(k)<0,则由题设对任意x∈N,f(x)∈N,得d(x)∈Z,于是有d(k)≤-1. 8分
由任意x∈N,d(x+1)≤d(x),所以-1≥d(k)≥d(k+1)≥d(k+2)≥ ≥d(k+n)≥ .,这里n是自然数. 于是有
d(k+n)+d(k+(n-1))+d(k+(n-2))+ +d(k)≤(n+1) d(k)≤(n+1)×(-1).
而d(k+n)+d(k+(n-1))+d(k+(n-2))+ +d(k)=f (k+n+1)-f (k),
所以f (k+n+1)-f (k)≤-(n+1).
取n=f (k),得f (k+f (k)+1)≤-f (k)-1+f (k)=-1,这与f (k+f (k)+1)∈N矛盾.
因此,必有对任意x∈N,d(x)≥0. 12分
(ⅱ)由(ⅰ)可知 d(1)≥d(2)≥d(3)≥ ≥d(n)≥ ≥0.
当d(1)=0时,则有d(1)=d(2)=d(3)= =d(n)=0,结论成立.
当d(1)≠0时,对任意n∈N,有d(n) ∈N,且d(n) ∈[0, d(1)].
因为在区间[0, d(1)]上的自然数只有有限个,而落在此区间上的自然数d(n)有无数多个,所以,必存在自然数c∈[0, d(1)]和无穷多个正整数n,满足d (n)=c. 16分
考点:不等式的证明
点评:关键是对于新定义的理解和准确的表示,属于中档题。审清题意,要仔细认真,避免误解。

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案