题目内容
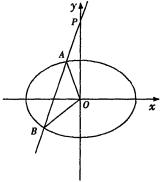
(21)已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线l过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
设椭圆方程为![]() =1(a>b>0).
=1(a>b>0).
(Ⅰ)由已知得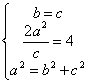
![]()
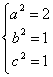 .
.
∴所求椭圆方程为![]() +y2=1.
+y2=1.
(Ⅱ)解法一:由题意知直线l的斜率存在,
设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),
由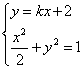 ,消去y得关于x的方程:
,消去y得关于x的方程:
(1+2k2)x2+8kx+6=0,
由直线l与椭圆相交于A、B两点,∴△>0 ![]() 64k2-24(1+2k2)>0,
64k2-24(1+2k2)>0,
解得 k2>![]() ,
,
又由韦达定理得 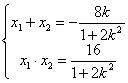
∴|AB|=![]() |x1-x2|=
|x1-x2|=![]()
![]()
=![]()
原点O到直线l的距离d=![]() .
.
∴S△AOB=![]() |AB|·d=
|AB|·d=![]() .
.
解法1:对S=![]() 两边平方整理得:
两边平方整理得:
4S2k4+4(S2-4)k2+S2+24=0 (*)
∵S≠0,
∴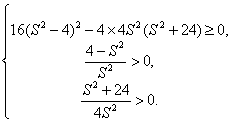
整理得:S2≤![]() .
.
又S>0,
∴0<S≤![]() .
.
从而S△AOB的最大值为S=![]() ,
,
此时代入方程(*)得
4k4-28k2+49=0
∴k=±![]()
所以,所求直线方程为:±![]() x-2y+4=0.
x-2y+4=0.
解法2:令m=![]() (m>0),
(m>0),
则2k2=m2+3.
∴S=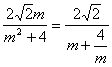 ≤
≤![]() .
.
当且仅当m=![]() 即m=2时,
即m=2时,
Smax=![]() .
.
此时k=±![]() .
.
所以,所求直线方程为±![]() x-2y+4=0.
x-2y+4=0.
解法二:由题意知直线l的斜率存在且不为零.
设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),
则直线l与x轴的交点D(-![]() ,0),
,0),
由解法一知 k2>![]() 且
且 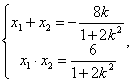
解法1:S△AOB=![]() |OD|·|y1-y2|=
|OD|·|y1-y2|=![]() |
|![]() |·|kx1+2-kx2-2|
|·|kx1+2-kx2-2|
=|x1-x2|
=![]()
=![]()
=![]() .
.
下同解法一.
解法2:S△AOB=S△POB-S△POA=![]() ×2×||x2|-|x1||=|x2-x1|=
×2×||x2|-|x1||=|x2-x1|=![]() .
.
下同解法一.

 阅读快车系列答案
阅读快车系列答案己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
 (Ⅰ)求切点
(Ⅰ)求切点 (1)求证:
(1)求证: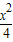 +
+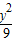 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程. ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 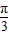 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.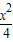 +
+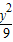 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.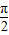 ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 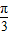 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.