题目内容
对于函数f(x)=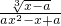 的定义域为全体实数,则实数a的取值范围是
的定义域为全体实数,则实数a的取值范围是
- A.(-
 ,
, )
) - B.(
 ,2)
,2) - C.(-∞,
 )∪(
)∪( ,+∞)
,+∞) - D.(-∞,0)∪(0,
 )
)
C
分析:函数的定义域为实数集即ax2-x+a≠0的解集为R;即ax2-x+a=0无解;令判别式小于0即可.
解答:因为f(x)的定义域为R
又f(x)有意义需ax2-x+a≠0
所以ax2-x+a=0无解
所以△=1-4a2<0且a≠0
解得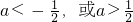
故选C
点评:本题考查等价转化的能力、考查二次方程解的个数取决于判别式.
分析:函数的定义域为实数集即ax2-x+a≠0的解集为R;即ax2-x+a=0无解;令判别式小于0即可.
解答:因为f(x)的定义域为R
又f(x)有意义需ax2-x+a≠0
所以ax2-x+a=0无解
所以△=1-4a2<0且a≠0
解得
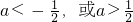
故选C
点评:本题考查等价转化的能力、考查二次方程解的个数取决于判别式.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
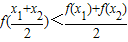 ;
; ;
;