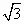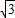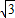题目内容
已知正方体的八个顶点中,有四个点恰好为正四面体的顶点,则该正四面体的体积与正方体的体积之比为
- A.1:

- B.1:3
- C.2:3
- D.1:2
B
分析:由题意可得该正四面体恰好以正方体的面对角线为棱,其体积为正方体的体积减掉4个相同的小三棱锥的体积,设出棱长可求.
解答:由题意可知该正四面体恰好以正方体的面对角线为棱,
故设正方体的棱长为a,则正四面体的棱长为 ,
,
而正方体的体积为a3,正四面体的体积为正方体的体积减掉4个相同的小三棱锥的体积,
故正四面体的体积为a3-4×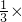
 ×a=
×a=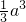
故该正四面体的体积与正方体的体积之比为: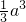 :a3=1:3
:a3=1:3
故选B
点评:本题考查体积公式,得到正四面体恰好以正方体的面对角线为棱是解决问题的关键,属基础题.
分析:由题意可得该正四面体恰好以正方体的面对角线为棱,其体积为正方体的体积减掉4个相同的小三棱锥的体积,设出棱长可求.
解答:由题意可知该正四面体恰好以正方体的面对角线为棱,
故设正方体的棱长为a,则正四面体的棱长为
 ,
,而正方体的体积为a3,正四面体的体积为正方体的体积减掉4个相同的小三棱锥的体积,
故正四面体的体积为a3-4×
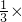
 ×a=
×a=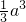
故该正四面体的体积与正方体的体积之比为:
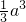 :a3=1:3
:a3=1:3故选B
点评:本题考查体积公式,得到正四面体恰好以正方体的面对角线为棱是解决问题的关键,属基础题.

练习册系列答案
相关题目