Question

若点（p，q）在|p|≤3，|q|≤3中按均匀分布出现．
（1）求方程x²+2px-q²+1=0有两个实数根的概率；
（2）若f(x)=x2+2

3

x+2，p，q∈Z，试求方程log|p+1.5|

q2+q+1

3

=|f(x)|，当0＜|p+1.5|＜1时恰有两个实根的概率．

Answer 1

分析：（1）作出题中不等式表示的正方形区域，算出其面积为36．方程x²+2px-q²+1=0有两个实数根，利用根的判别式算出p²+q²≥1，得到满足条件的区域为正方形内部且在单位圆外的阴影部分，算出其面积为36-π．最后利用几何概型计算公式，可得所求概率；
（2）由一元二次不等式的解法，可得p、q∈{-3，-2，-1，0，1，2，3}，因此所有的（p，q）共有7×7=49个．再设y₁=log|p+1.5|

q2+q+1

3

，y₂=|f（x）|，利用函数图象加以讨论并结合对数的运算法则加以计算，可得符合条件“恰有两个实根”的情况总共有8种，由此利用古典概型公式加以计算，即可得到所求概率．

解答：解：（1）|p|≤3，|q|≤3表示一个正方形区域，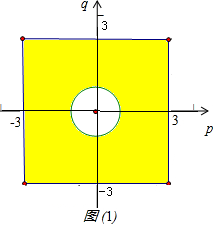
如右图所示，可得其面积为S=6×6=36．
若方程x²+2px-q²+1=0有两个实数根，
则△=（2p²）-4（-q²+1）≥0，即p²+q²≥1，
相应的区域为正方形内部且在单位圆外，其面积为S₁=36-π，
即方程x²+2px-q²+1=0有两个实数根的概率为P₁=

S1

S

=

36-π

36

．
（2）∵f(x)=x2+2

3

x+2=[x+（

3

+1）][x+（

3

-1）]，
（其中p、q∈Z）
∴p、q∈{-3，-2，-1，0，1，2，3}，
所有的（p，q）共有7×7=49个．
设y₁=log|p+1.5|

q2+q+1

3

，y₂=|f（x）|，
其中y₁ 表示一条与x轴平行或重合的直线，y₂表示的曲线如下图所示．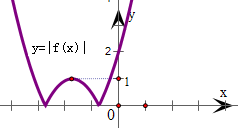
要使得原方程有两个实根，则y₁与y₂的图象有且仅有2个交点，可得y₁=0或y₁＞1，
又∵0＜|p+1.5|＜1，∴-2.5＜p＜-0.5，得p=-2或p=-1．
①若y₁=0，则log|p+1.5|

q2+q+1

3

=0，可得

q2+q+1

3

=1，
即q²+q-2=0，解之得q=1或q=-2，
故符合方程有两个实根的情况有（-2，1），（-2，-2 ），（-1，1），（-1，-2），共4种情况．
②若y₁＞1，则log|p+1.5|

q2+q+1

3

＞1，可得

q2+q+1

3

＜|p+1.5|，
即

q2+q+1

3

＜0.5，解之得q=-1或q=0，
故符合方程有两个实根的情况有：（-2，-1），（-2，0 ），（-1，-1），（-1，0）有共4种情况．
综上所述，符合方程有两个实根的情况共有8种，
因此，方程log|p+1.5|

q2+q+1

3

=|f(x)|当0＜|p+1.5|＜1时恰有两个实根的概率为P₂=

8

49

．

点评：本题主要考查几何概型、古典概型的应用，考查了函数与方程的综合应用等知识，属于中档题．用列举法计算可列举事件中的基本事件，运用等价转化和数形结合的数学思想，是解决本题的关键．