题目内容
1．利用“五点法”做函数y=2sinx在[0，2π]上的图象．分析 利用“五点法”即可作出函数y=f（x）在一个周期上的图象
解答 解：列表：
| x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sinx | 0 | 1 | 0 | -1 | 0 |
| y=2sinx | 0 | 2 | 0 | -2 | 0 |
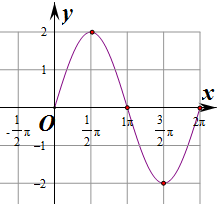
点评 本题主要考查三角函数的图象和性质，要求熟练掌握五点法作图的基本方法．
练习册系列答案
相关题目
12．下列说法正确的是（ ）
| A． | ?x∈R，x2＞0 | |
| B． | ?x0∈R，x02-x0+1≤0 | |
| C． | “a＞b”是“ac2＞bc2”的充分条件 | |
| D． | △ABC为等边三角形的充要条件是a2+b2+c2=ab+bc+ac |
16．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1右焦点F作一条直线，当直线斜率为2时，直线与双曲线左、右两支各有一个交点；当直线斜率为3时，直线与双曲线右支有两个不同交点，则双曲线离心率的取值范围是（ ）
| A． | （1，$\sqrt{2}$） | B． | （1，$\sqrt{2}$+1） | C． | （$\sqrt{2}$+1，$\sqrt{10}$） | D． | （$\sqrt{5}$，$\sqrt{10}$） |
如图所示，已知D、E、F分别是△ABC的边BC、CA、AB的中点，P是△ABC内任意一点，求证：$\overrightarrow{PD}$+$\overrightarrow{PE}$+$\overrightarrow{PF}$=$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$．