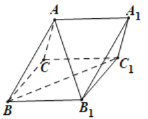
题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)互相平行的两条直线![]() 分别过
分别过![]() ,且直线
,且直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若四边形
两点,若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)直线
(2)直线![]() 的方程为
的方程为![]() 或
或![]() ;相应地,直线
;相应地,直线![]() 的方程
的方程![]() 或
或![]()
【解析】
![]() 由题意知
由题意知![]() ,结合离心率和
,结合离心率和![]() 之间的关系即可求解;
之间的关系即可求解;
![]() 由
由![]() 知,
知,![]() , 由对称性知四边形
, 由对称性知四边形![]() 为平行四边形,分斜率存在和不存在两种情况分别求出四边形
为平行四边形,分斜率存在和不存在两种情况分别求出四边形![]() 的面积的表达式,进而求出直线方程.
的面积的表达式,进而求出直线方程.
![]() 由题意知
由题意知![]() ,因为椭圆
,因为椭圆![]() 的离心率为
的离心率为![]() ,
,
所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1)知焦点![]() 的坐标为
的坐标为![]() ,
,
①当直线![]() 的斜率不存在时,其直线方程分别是
的斜率不存在时,其直线方程分别是![]() ,
,
将![]() 代入椭圆
代入椭圆![]() ,得
,得![]() ,解得
,解得![]() ,
,
所以![]() 的坐标分别为
的坐标分别为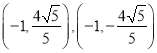 或
或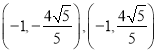 ;
;
同理可得,![]() 的坐标分别为
的坐标分别为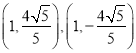 或
或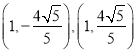 ;
;
则四边形![]() 的面积
的面积![]() 不合题意,
不合题意,
②当直线![]() 的斜率存在时,设此时直线
的斜率存在时,设此时直线![]() 的方程分别为
的方程分别为![]() .
.
联立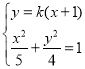 消去
消去![]() ,得
,得![]() ,
,
设点![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
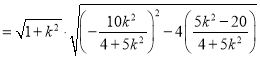
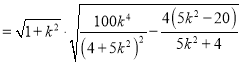
![]() .
.
而直线![]() 之间的距离为
之间的距离为![]() ,
,
由对称性知四边形![]() 为平行四边形,
为平行四边形,
所以四边形![]() 的面积为
的面积为
 ,
,
又四边形![]() 的面积为
的面积为![]() ,所以
,所以![]() ,
,
得![]() ,平方
,平方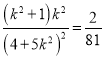 ,化简得
,化简得![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,所以
,所以![]() ,
,
故直线![]() 的方程为
的方程为![]() 或
或![]() ;相应地,直线
;相应地,直线![]() 的方程
的方程![]() 或
或![]() .
.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案【题目】从30个个体中抽取10个个体,并将这30个个体编号00,01,…,29.现给出某随机数表的第11行到第15行(见下表),如果某人选取第12行的第6列和第7列中的数作为第1个数并且由此数向右读,则选取的前4个的号码分别为( )
9264 | 4607 | 2021 | 3920 | 7766 | 3817 | 3256 | 1640 |
5858 | 7766 | 3170 | 0500 | 2593 | 0545 | 5370 | 7814 |
2889 | 6628 | 6757 | 8231 | 1589 | 0062 | 0047 | 3815 |
5131 | 8186 | 3709 | 4521 | 6665 | 5325 | 5383 | 2702 |
9055 | 7196 | 2172 | 3207 | 1114 | 1384 | 4359 | 4488 |
A.76,63,17,00B.16,00,02,30C.17,00,02,25D.17,00,02,07