题目内容
2.已知cos(-$\frac{π}{2}$+α)=-$\frac{4}{5}$,且α∈(π,$\frac{3π}{2}$),则tanα=$\frac{4}{3}$.分析 利用诱导公式化简已知条件,利用同角三角函数的基本关系式求解即可.
解答 解:cos(-$\frac{π}{2}$+α)=cos($\frac{π}{2}-α$)=-$\frac{4}{5}$,且α∈(π,$\frac{3π}{2}$),
可得sinα=-$\frac{4}{5}$.cosα=$-\sqrt{1-{sin}^{2}α}$=-$\frac{3}{5}$,
tanα=$\frac{sinα}{cosα}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查诱导公式以及同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
相关题目
7.下列命题中,正确命题的序号为( )
| A. | 命题p:?x∈R,使得x2-1≥0,命题q:?x∈R,使得x2-x-1≥0,则命题p∨¬q是假命题 | |
| B. | 非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,“$\overrightarrow{a}$•$\overrightarrow{b}$>0”是“$\overrightarrow{a}$与$\overrightarrow{b}$夹角是锐角”的充要条件 | |
| C. | “两直线2x-my-1=0与x+my-1=0垂直”是“$m=±\sqrt{2}$”的充要条件 | |
| D. | “a=1”是“函数f(x)=x2+|x+a-1|(x∈R)为偶函数”的充分不必要条件 |
11.设非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则θ∈($\frac{π}{2}$,π)是$\overrightarrow{a}$•$\overrightarrow{b}$<0的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,在圆柱EF中,底面圆的半径为2,母线长为6,$\widehat{AB}$和$\widehat{CD}$的长均为所在圆的周长的$\frac{1}{6}$,若沿着面ABCD将圆柱截开,试求所截得的体积较小的几何体的体积V.
如图,在圆柱EF中,底面圆的半径为2,母线长为6,$\widehat{AB}$和$\widehat{CD}$的长均为所在圆的周长的$\frac{1}{6}$,若沿着面ABCD将圆柱截开,试求所截得的体积较小的几何体的体积V.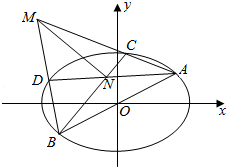 如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N. 直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1点的中点,且AA1=AC=BC=$\frac{\sqrt{2}}{2}$AB.
直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1点的中点,且AA1=AC=BC=$\frac{\sqrt{2}}{2}$AB.