题目内容
矩阵A=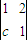
的一个特征值为λ，
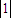是A的属于特征值λ的一个特征向量，则A-1= ．
【答案】分析：根据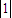
是A的属于特征值λ的一个特征向量得到矩阵A中的c的值，利用主对角元互换，次对角元变号求出矩阵A的伴随矩阵A*，然后利用A-1=
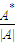求出矩阵A的逆矩阵即可．
解答：解：由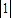
是A的属于特征值λ的一个特征向量，得到c=0，
所以A=
=1，则A-1=
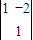
故答案为：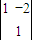
点评：此题要求学生掌握矩阵的特征向量和特征值，会求二阶矩阵的伴随矩阵，会根据伴随矩阵求矩阵的逆矩阵，是一道综合题．
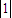是A的属于特征值λ的一个特征向量得到矩阵A中的c的值，利用主对角元互换，次对角元变号求出矩阵A的伴随矩阵A*，然后利用A-1=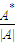求出矩阵A的逆矩阵即可．解答：解：由
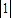是A的属于特征值λ的一个特征向量，得到c=0，所以A=
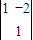
=1，则A-1=故答案为：
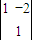
点评：此题要求学生掌握矩阵的特征向量和特征值，会求二阶矩阵的伴随矩阵，会根据伴随矩阵求矩阵的逆矩阵，是一道综合题．
练习册系列答案
相关题目
,A的一个特征值
，其对应的特征向量是
.
；
，计算
的值.
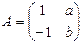,A的一个特征值
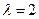，属于λ的特征向量是
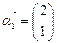,求矩阵A与其逆矩阵.
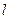的极坐标方程是
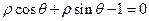．以极点为平面直角坐标系的原点，极轴为
轴的正半轴，建立平面直角坐标系，在曲线
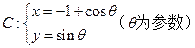上求一点，使它到直线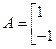
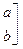,A的一个特征值
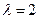，其对应的特征向量是
.
；
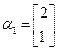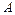在矩阵M所对应的线性变换下的像的方程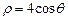
．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：
，
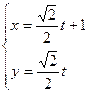求直线l与曲线C相交所成的弦的弦长．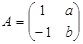
,A的一个特征值
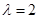，属于λ的特征向量是
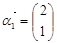,求矩阵A与其逆矩阵.