题目内容
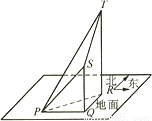
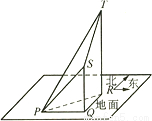
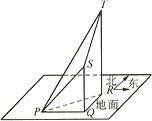 一气球以V(m/s)的速度由地面上升,10分钟后由观察点P测得气球在P的正东方向S处,仰角为45°;再过10分钟后,测得气球在P的东偏北30°方向T处,其仰角为60°(如图,其中Q、R分别为气球在S、T处时的正投影).求风向和风速(风速用V表示).
一气球以V(m/s)的速度由地面上升,10分钟后由观察点P测得气球在P的正东方向S处,仰角为45°;再过10分钟后,测得气球在P的东偏北30°方向T处,其仰角为60°(如图,其中Q、R分别为气球在S、T处时的正投影).求风向和风速(风速用V表示).
分析:依题意可知即∠SPQ=
,∠RPQ=
,∠TPR=
,进而可知PQ=QS,RT=2QS,进而根据PR=RT•cot
求得PR,进而根据余弦定理求得QR,推断出PR2=PQ2+QR2,可知∠PQR=
,求得答案.
| π |
| 4 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
解答:解:10分钟后由观察点P测得气球在P的正东方向,仰角为45°的S点处,
即∠SPQ=
,所以PQ=QS=600V(m).
又10分钟后测得气球在P的东偏北30°,其仰角为60°的T点处,
即∠RPQ=
,∠TPR=
,RT=2QS=1200V(m),
于是PR=RT•cot
=400
V(m).
在△PQR中由余弦定理得:QR=
=200
(m).
因为PR2=(400
V)2=(600V)2+(200
V)2=PQ2+QR2,所以∠PQR=
,
即风向为正南风.
因为气球从S点到T点经历10分钟,即600s,
所以风速为
=
(m/s).
答:风向为正南风,风速为
m/s.
即∠SPQ=
| π |
| 4 |
又10分钟后测得气球在P的东偏北30°,其仰角为60°的T点处,
即∠RPQ=
| π |
| 6 |
| π |
| 3 |
于是PR=RT•cot
| π |
| 3 |
| 3 |
在△PQR中由余弦定理得:QR=
| PQ2+PR2-2PQ•PRcos∠QPR |
| 3 |
因为PR2=(400
| 3 |
| 3 |
| π |
| 2 |
即风向为正南风.
因为气球从S点到T点经历10分钟,即600s,
所以风速为
| |QR| |
| 600 |
| ||
| 3 |
答:风向为正南风,风速为
| ||
| 3 |
点评:本题主要考查了解三角形的实际应用.解题的关键是找到PR,PQ和QR三边之间的关系.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目