题目内容
(18乙)如图,已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.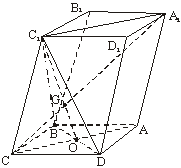
(Ⅰ)证明:C1C⊥BD;
(Ⅱ)当![]() 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
(18乙)本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力.

(1)证明:连结A1C1、AC,AC和BD交于O,连结C1O.
∵四边形ABCD是菱形,
∴AC⊥BD,BC=CD.
又∵∠BCC1=∠DCC1,C1C=C1C,
∴△C1BC≌△C1DC,
∴C1B=C1D,
∵DO=OB,
∴C1O⊥BD,
但,AC⊥BD,AC∩C1O=O,
∴BD⊥平面AC1.
又C1C![]() 平面AC1,
平面AC1,
∴C1C⊥BD.
(Ⅱ)当![]() 时,能使A1C⊥平面C1BD.
时,能使A1C⊥平面C1BD.
证明一:
∵![]() ,
,
∴BC=CD=C1C.
又∠BCD=∠C1CB=∠C1CD,
由此可推得BD=C1B=C1D.
∴三棱锥C—C1BD是正三棱锥.
设A1C与C1O相交于G.
∵A1C1∥AC,且A1C1∶OC=2∶1,
∴C1G∶GO=2∶1.
又C1O是正三角形C1BD的BD边上的高和中线,
∴点G是正三角形C1BD的中心,
∴CG⊥平面C1BD.即 A1C⊥平面C1BD.
证明二:
由(Ⅰ)知,BD⊥平面AC1,
∵A1C![]() 平面AC1,∴BD⊥A1C.
平面AC1,∴BD⊥A1C.
当![]() 时,平行六面体的六个面是全等的菱形,
时,平行六面体的六个面是全等的菱形,
同BD⊥A1C的证法可得BC1⊥A1C.
又BD∩BC1=B,
∴A1C⊥平面C1BD.

练习册系列答案
相关题目
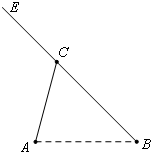 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出. (2011•潍坊二模)2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏,某国际组织计划派出12名心理专家和18名核专家赴日本工作,临行前对这30名专家进行了总分为1000分的综合素质测评,测评成绩用茎叶图进行了记录,如图(单位:分).规定测评成绩在976分以上(包括976)为“尖端专家”,测评成绩在976分以下为“高级专家”,且只有核专家中的“尖端专家”才可以独立开展工作,这些专家先飞抵日本的城市E,再分乘三辆汽车到达工作地点福岛县.已知从城市E到福岛县有三条公路,因地震破坏了道路,汽车可能受阻.据了解:汽车走公路I和公路II顺利到达的概率都为
(2011•潍坊二模)2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏,某国际组织计划派出12名心理专家和18名核专家赴日本工作,临行前对这30名专家进行了总分为1000分的综合素质测评,测评成绩用茎叶图进行了记录,如图(单位:分).规定测评成绩在976分以上(包括976)为“尖端专家”,测评成绩在976分以下为“高级专家”,且只有核专家中的“尖端专家”才可以独立开展工作,这些专家先飞抵日本的城市E,再分乘三辆汽车到达工作地点福岛县.已知从城市E到福岛县有三条公路,因地震破坏了道路,汽车可能受阻.据了解:汽车走公路I和公路II顺利到达的概率都为