题目内容
已知数列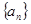 的前n项和为
的前n项和为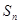 ,
,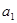 =1,且
=1,且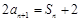
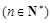 .
.
(1)求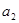 ,
,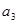 的值,并求数列
的值,并求数列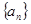 的通项公式;
的通项公式;
(2)解不等式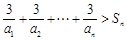
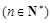 .
.
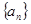 的前n项和为
的前n项和为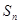 ,
,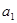 =1,且
=1,且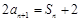
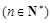 .
.(1)求
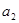 ,
,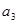 的值,并求数列
的值,并求数列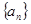 的通项公式;
的通项公式;(2)解不等式
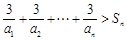
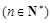 .
.(1)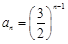 (2)根据数列的规律性,通过放缩法来得到证明。
(2)根据数列的规律性,通过放缩法来得到证明。
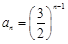 (2)根据数列的规律性,通过放缩法来得到证明。
(2)根据数列的规律性,通过放缩法来得到证明。试题分析:(1)∵
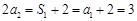 ,∴
,∴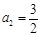 . 1分
. 1分∵
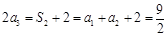 ,∴
,∴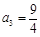 . 2分
. 2分∵
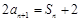 ,∴
,∴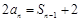 (n≥2),
(n≥2),两式相减,得
 .
.∴
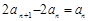 .则
.则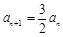 (n≥2). 4分
(n≥2). 4分∵
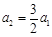 ,∴
,∴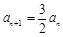
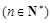 . 5分
. 5分∵
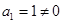 ,∴
,∴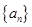 为等比数列,
为等比数列,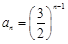 . 7分
. 7分(2)
 ,
,∴数列
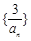 是首项为3,公比为
是首项为3,公比为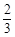 等比数列. 8分
等比数列. 8分数列
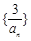 的前5项为:3,2,
的前5项为:3,2,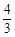 ,
,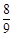 ,
,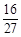 .
.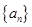 的前5项为:1,
的前5项为:1,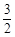 ,
,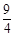 ,
,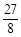 ,
,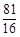 .
.∴n=1,2,3时,
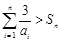 成立; 11分
成立; 11分而n=4时,
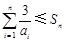 ; 12分
; 12分∵n≥5时,
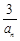 <1,an>1,∴
<1,an>1,∴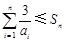 . 14分
. 14分∴不等式
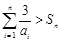
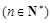 的解集为{1,2,3}. 16分
的解集为{1,2,3}. 16分点评:解决的关键是能熟练的根据等比数列的通项公式来得到表达式,同时能结合不等式的性质来放缩得到证明,属于中档题。

练习册系列答案
相关题目
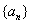 是等差数列
是等差数列 ,
, ,
, 项和为
项和为 ,则使得
,则使得 中,
中, ,则
,则 等于( )
等于( )



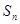 是等差数列
是等差数列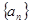 的前
的前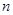 项和,若
项和,若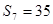 ,则
,则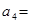 ___________。
___________。 中,
中, ,则
,则 ( )
( )


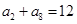 ,则
,则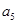 等于( ).
等于( ). 中,
中,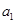 +
+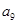 =10则
=10则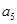 的值为
的值为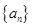 的前
的前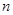 项和为
项和为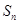 ,且方程
,且方程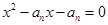 有一个根为
有一个根为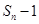 ,
,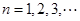 .
.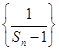 是等差数列;
是等差数列;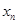 ,数列
,数列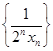 的前
的前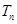 ,求
,求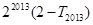 的值;
的值;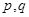 ,使得
,使得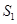 ,
,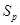 ,
,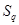 成等比数列,若存在,求出满足条件的
成等比数列,若存在,求出满足条件的