题目内容
已知a、b、c是△ABC的三条边,它们所对的角分别是A、B、C,若a、b、c成等比数列,且a2-c2=ac-bc,试求
⑴角A的度数;
⑵求证: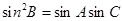 ;
;
(3)求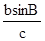 的值.
的值.
⑴角A的度数;
⑵求证:
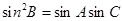 ;
;(3)求
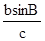 的值.
的值.(1)根据题意,由于a、b、c成等比数列,且a2-c2=ac-bc,结合余弦定理来得到求解。
(2)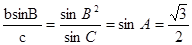
(2)
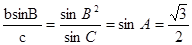
试题分析:⑴∵a、b、c成等比数列 ∴
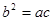 ∵a2-c2=ac-bc ∴a2-c2=
∵a2-c2=ac-bc ∴a2-c2=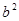 -bc
-bc ∴
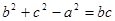 ∴
∴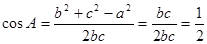 又 ∵
又 ∵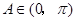
∴
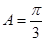 (7分)
(7分)(2)

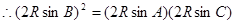
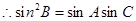 (10分)
(10分)(3)
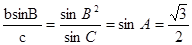
点评:解决的关键是借助于等比数列来得到a,b,c得关系,结合余弦定理得到角,同事能结合正弦定理得到求解,属于基础题。

练习册系列答案
相关题目
 中,角A、B的对边分别为
中,角A、B的对边分别为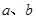 ,
, 
 则
则 = .
= .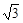 bc.
bc. 。
。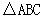 中,内角A,B,C所对的分别是a, b,c。已知a=2.c=
中,内角A,B,C所对的分别是a, b,c。已知a=2.c=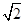 ,
, 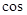 A=
A=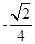 .
.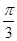 )的值.
)的值.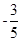 ,则三角形的第三边长为( )
,则三角形的第三边长为( )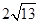 C、16 D、4
C、16 D、4 中,
中, ,
, ,
, ,则最短边的边长等于( )
,则最短边的边长等于( )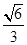



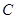 与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30
与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30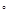 ,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为
,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为 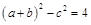 ,且C=60°,则ab的值为________________.
,且C=60°,则ab的值为________________.