题目内容
设直线方程为l:(a+1)x+y+2+a=0(a∈R)(Ⅰ)若直线l在两坐标轴上的截距相等,求直线l方程;
(Ⅱ)若l不经过第二象限,求实数a的取值范围.
【答案】分析:(Ⅰ)根据直线方程求出它在两坐标轴上的截距,根据它在两坐标轴上的截距相等,求出a的值,即得直线l方程.
(Ⅱ)把直线方程化为斜截式为 y=-(a+1)x-a-2,若l不经过第二象限,则a=-1 或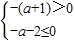 ,由此求得实数a的取值范为.
,由此求得实数a的取值范为.
解答:解:(Ⅰ)直线方程为l:(a+1)x+y+2+a=0(a∈R),令x=0可得 y=-a-2;令y=0可得x=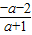 ,
,
若直线l在两坐标轴上的截距相等,则-a-2=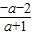 ,解得 a=0或 a=-2,
,解得 a=0或 a=-2,
故直线l方程为 x+y+2=0 或 x-y=0.
(Ⅱ)∵直线方程为 y=-(a+1)x-a-2,若l不经过第二象限,则a=-1 或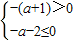 ,
,
解得-2≤a≤-1,故实数a的取值范围为[-2,-1].
点评:本题主要考查直线方程的一般式,直线在坐标轴上的截距的定义,直线在坐标系中的位置与它的斜率、截距的关系,属于基础题.
(Ⅱ)把直线方程化为斜截式为 y=-(a+1)x-a-2,若l不经过第二象限,则a=-1 或
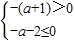 ,由此求得实数a的取值范为.
,由此求得实数a的取值范为.解答:解:(Ⅰ)直线方程为l:(a+1)x+y+2+a=0(a∈R),令x=0可得 y=-a-2;令y=0可得x=
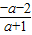 ,
,若直线l在两坐标轴上的截距相等,则-a-2=
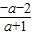 ,解得 a=0或 a=-2,
,解得 a=0或 a=-2,故直线l方程为 x+y+2=0 或 x-y=0.
(Ⅱ)∵直线方程为 y=-(a+1)x-a-2,若l不经过第二象限,则a=-1 或
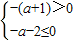 ,
,解得-2≤a≤-1,故实数a的取值范围为[-2,-1].
点评:本题主要考查直线方程的一般式,直线在坐标轴上的截距的定义,直线在坐标系中的位置与它的斜率、截距的关系,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,A,B是椭圆
如图,A,B是椭圆