题目内容
在直线l:x-y+9=0上任取一点P,过点P以椭圆
解:设所求椭圆的方程为![]() =1,与x-y+9=0联立得(2a2-9)x2+18a2x+90a2-a4=0,点P在直线x-y+9=0上,所以Δ=(18a2)2-4(2a2-9)(90a2-a4)≥0,即a4-54a2+405≥0.解之得a2≥45或a2≤9,因为a>c=3,所以a2≥45.所以椭圆的长轴最短时的方程为
=1,与x-y+9=0联立得(2a2-9)x2+18a2x+90a2-a4=0,点P在直线x-y+9=0上,所以Δ=(18a2)2-4(2a2-9)(90a2-a4)≥0,即a4-54a2+405≥0.解之得a2≥45或a2≤9,因为a>c=3,所以a2≥45.所以椭圆的长轴最短时的方程为![]() =1.联立
=1.联立![]() =1和x-y+9=0得点P(-5,4).
=1和x-y+9=0得点P(-5,4).
点拨:利用判别式可以确定参数的取值范围,再加以讨论便可得到最后的结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
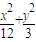 =1的焦点为焦点作椭圆.
=1的焦点为焦点作椭圆.