题目内容
在直线L:x-y+9=0上任取一点p以椭圆| x2 |
| 12 |
| y2 |
| 3 |
(1)p在何处时,所求椭圆的长轴最短;
(2)求长轴最短的椭圆方程.
分析:先求出椭圆的焦点,根据椭圆的定义可知要使长轴长最短,实际上就是在直线x-y+9=0上找一点M,到F1,F2的距离之和最小.设F1关于x-y+9=0的对称点是A(t,s),则根据点关于直线对称点的求法求得A点坐标,进而求得A点在(-5,4)处时,长轴最短,进而求得b,则此时椭圆的方程可得.
解答:解:(1)可知焦点是F1(-3,0),F2(3,0).由椭圆定义可知长轴长2a=|PF1|+|PF2|
要使长轴长最短,实际上就是在直线x-y+9=0上找一点M,到F1,F2的距离之和最小.
设F1关于x-y+9=0的对称点是A(t,s),
则
-
+9=0,
又
=-1,
解得t=-9,s=6,即A(-9,6),
,此时P(-5,4).
(2)由(1)可知最短长轴长是|AF2|=6
由a=3
,c=3得b=6
所以方程为
+
=1
要使长轴长最短,实际上就是在直线x-y+9=0上找一点M,到F1,F2的距离之和最小.
设F1关于x-y+9=0的对称点是A(t,s),
则
| t-3 |
| 2 |
| s |
| 2 |
又
| s |
| t+3 |
解得t=-9,s=6,即A(-9,6),
|
(2)由(1)可知最短长轴长是|AF2|=6
| 5 |
由a=3
| 5 |
所以方程为
| x2 |
| 45 |
| y2 |
| 36 |
点评:本题主要考查了椭圆的标准方程问题.涉及了椭圆的定义,点关于直线的对称问题等,综合性很强.

练习册系列答案
相关题目
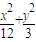 =1的焦点为焦点作椭圆.
=1的焦点为焦点作椭圆.