题目内容
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足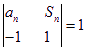 (
(![]() 为正整数).
为正整数).
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() .试比较
.试比较![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(1)![]() (2)
(2)![]()
解析:
(1)![]() ,
,
![]()
以上两式相减得到![]() ,即
,即![]() 3分
3分
所以![]() ,数列
,数列![]() 是公比为
是公比为![]() 等比数列,又
等比数列,又![]() ,
,![]() ,
,
所以![]() . 6分
. 6分
(2)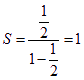 ,
,![]() 8分
8分
设![]() ,则
,则![]() ,
,![]()
![]() =
=![]() <0
<0
所以,函数f(n)在n??N*上单调递减,所以f(n)的最大值是f(1)=1,
所以. 12分

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式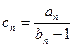 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.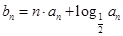 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.