题目内容
已知函数![]() 在
在![]() 上单调递减,在(1,3)上单调递增在
上单调递减,在(1,3)上单调递增在![]() 上单调递减,且函数图象在
上单调递减,且函数图象在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求实数![]() 、
、![]() 、
、![]() 的值;(Ⅱ)设函数
的值;(Ⅱ)设函数![]() =0有三个不相等的实数根,求
=0有三个不相等的实数根,求![]() 的取值范围.
的取值范围.
(Ⅰ)![]() ,
,![]() ,
,![]() .(Ⅱ)
.(Ⅱ)![]()
解析:
(Ⅰ)![]() ,∵函数图象在
,∵函数图象在![]() 处的切线与直线
处的切线与直线![]() 垂直,∴
垂直,∴![]() .①
.①
由已知可知,1和3为方程![]() 的两根,所以
的两根,所以
![]() ②
②![]() ③
③
由①、②、③解得![]() ,
,![]() ,
,![]() .…6分
.…6分
(Ⅱ)由(Ⅰ)得![]() ,
,
![]() 和
和![]() 分别是函数
分别是函数![]() 的极小值点和极大值点,且当
的极小值点和极大值点,且当![]() 取负值且绝对值足够大时,
取负值且绝对值足够大时,![]() 取正值,当
取正值,当![]() 时正值且足够大时,
时正值且足够大时,![]() 取负值.……8分
取负值.……8分
所以方程![]() 有三个不相等的实数根的充要条件为
有三个不相等的实数根的充要条件为
![]() 即
即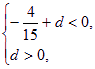 所以
所以![]() 的取值范围为
的取值范围为![]() …12分
…12分

练习册系列答案
相关题目
 在
在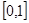 上单调递减且满足
上单调递减且满足 .
. 的取值范围.
的取值范围. ,求
,求 在
在 在
在 上单调递减,则
上单调递减,则 的取值范围
的取值范围 B.
B. C.
C. D.
D.
 在
在 上单调递减,且满足
上单调递减,且满足 ,
, (Ⅰ) 求
(Ⅰ) 求 的取值范围;(Ⅱ)设
的取值范围;(Ⅱ)设 ,求在
,求在 在
在 上单调递减,则
上单调递减,则 的取值范围是
的取值范围是