题目内容
已知函数 在
在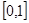 上单调递减且满足
上单调递减且满足 .
.
(1)求 的取值范围.
的取值范围.
(2)设 ,求
,求 在
在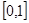 上的最大值和最小值.
上的最大值和最小值.
【答案】
(1)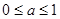 ;(2)当
;(2)当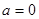 时,
时,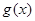 在
在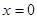 取得最小值
取得最小值 ,
,
在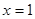 上取得最大值
上取得最大值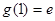 .
.
当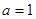 时,
时,
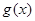 在
在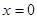 取得最大值
取得最大值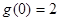 ,在
,在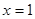 时取得最小值
时取得最小值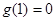 .
.
当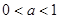 时,由
时,由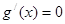 ,得
,得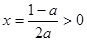 .
.
当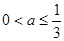 时,
时,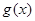 在
在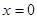 时取得最小值
时取得最小值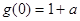 ,在
,在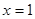 时取得最大值
时取得最大值 .
.
当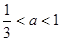 时,
时,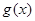 在
在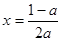 时取得最大值
时取得最大值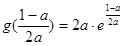 ,在
,在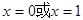 时取得最小值,
时取得最小值,
当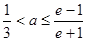 时,
时,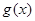 在
在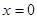 时取得最小值
时取得最小值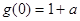 ;
;
当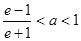 时,
时,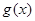 在
在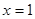 时取得最小值
时取得最小值 .
.
【解析】
试题分析:(1)注意到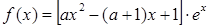 ,
,
其导函数为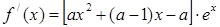
根据题意得到“对于任意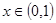 .有
.有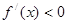 ”.所以结合二次函数的性质分类讨论.
”.所以结合二次函数的性质分类讨论.
具体情况有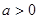 ,
,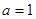 ,
,
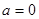 ,
,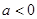 .
.
(2)注意到 ,
,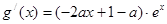 ,
,
讨论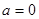 ,
,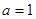 ,
,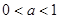 的情况.
的情况.
而在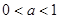 时,要结合二次函数的图象和性质,具体地讨论①若
时,要结合二次函数的图象和性质,具体地讨论①若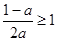 ,即
,即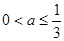 ;
;
②若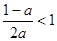 ,即
,即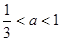 的不同情况.
的不同情况.
易错点在于分类讨论不全面.
试题解析:
(1)由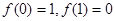 得:
得: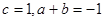
则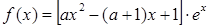 ,
,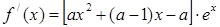
依题意需对于任意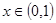 .有
.有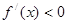 .
.
当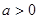 时,因为二次函数
时,因为二次函数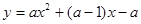 的图像开口向上,
的图像开口向上,
而 ,所以需
,所以需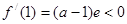 ,即
,即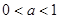 ;
;
当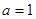 时,对任意
时,对任意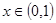 有
有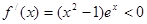 ,
, 符合条件;
符合条件;
当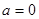 时,对任意
时,对任意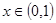 有
有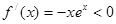 ,
, 符合条件;
符合条件;
当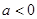 时,因为
时,因为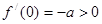 ,
, 不符合条件.
不符合条件.
故 的取值范围为
的取值范围为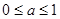 .
.
(2)因 ,
,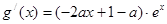 ,
,
当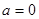 时,
时,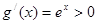 ,
,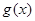 在
在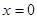 取得最小值
取得最小值 ,
,
在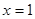 上取得最大值
上取得最大值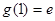 .
.
当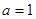 时,对任意
时,对任意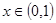 有
有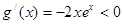 ,
,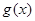 在
在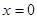 取得最大值
取得最大值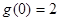 ,在
,在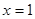 时取得最小值
时取得最小值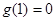 .
.
当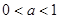 时,由
时,由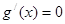 ,得
,得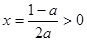 .
.
①若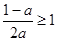 ,即
,即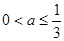 时,
时,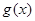 在
在 上单调递增,
上单调递增,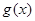 在
在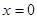 时取得最小值
时取得最小值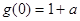 ,在
,在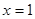 时取得最大值
时取得最大值 .
.
②若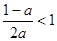 ,即
,即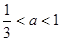 时,
时,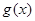 在
在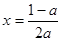 时取得最大值
时取得最大值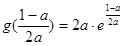 ,在
,在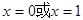 时取得最小值,而
时取得最小值,而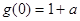 ,
, .则当
.则当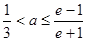 时,
时,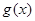 在
在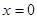 时取得最小值
时取得最小值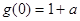 ;
;
当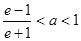 时,
时,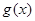 在
在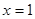 时取得最小值
时取得最小值 .
.
考点:应用导数研究函数,分类讨论思想,数学式子的变形能力.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 在
在 上单调递减,则
上单调递减,则 的取值范围
的取值范围 B.
B. C.
C. D.
D.
 在
在 上单调递减,且满足
上单调递减,且满足 ,
, (Ⅰ) 求
(Ⅰ) 求 的取值范围;(Ⅱ)设
的取值范围;(Ⅱ)设 ,求在
,求在 在
在 上单调递减,则
上单调递减,则 的取值范围是
的取值范围是