题目内容
甲、乙二人从A地沿同一方向去B地,途中都使用两种不同的速度 与
与 (
( <
< ). 甲前一半的路程使用速度
). 甲前一半的路程使用速度 ,后一半的路程使用速度
,后一半的路程使用速度 ;乙前一半的时间使用速度
;乙前一半的时间使用速度 ,后一半时间使用速度
,后一半时间使用速度 .关于甲、乙二人从A地到达B地的路程与时间的函数图象及关系,有如图所示的四个不同的图示分析(其中横轴
.关于甲、乙二人从A地到达B地的路程与时间的函数图象及关系,有如图所示的四个不同的图示分析(其中横轴 表示时间,纵轴
表示时间,纵轴 表示路程,C是AB的中点),则其中可能正确的图示分析为 ( )
表示路程,C是AB的中点),则其中可能正确的图示分析为 ( )
| A.(1) | B.(2) | C.(3) | D.(4) |
A
解析解:∵甲乙开始时都以速度v1行走,∴在起始一段时间里甲乙所走的路程随时间变化图象重合.
由已知,甲一半路程使用速度v1,另一半路程使用速度v2
∵v1<v2∴甲走一半路程所用时间t>t1.乙前一半时间行走路程不到总路程的一半.
故选A.

练习册系列答案
相关题目
已知函数 是偶函数,
是偶函数, 在
在 内单调递增,则实数
内单调递增,则实数 ( )
( )
A. | B. | C.0 | D.2 |
若 ,那么
,那么 的最大值是
的最大值是
A. | B. | C.1 | D.2 |
设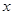 为实数,则
为实数,则 与
与 表示同一个函数的是 (▲)
表示同一个函数的是 (▲)
A. | B. |
C.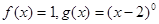 | D. |
下列函数中,与函数 相同的是 ( )
相同的是 ( )
A. | B. | C. | D. |
函数 的值域为
的值域为
A. | B. | C. | D. |
 ②
② ③
③ ④
④ 的图象(部分)如下,则按照从左到右图像对应的函数序号安排正确的一组是 ( )
的图象(部分)如下,则按照从左到右图像对应的函数序号安排正确的一组是 ( )
 的图像分别如图1、2所示.函数
的图像分别如图1、2所示.函数 . 则以下有关函数
. 则以下有关函数 的性质中,错误的是(▲)
的性质中,错误的是(▲)  处没有意义;
处没有意义;