题目内容
下列函数中,与函数 相同的是 ( )
相同的是 ( )
A. | B. | C. | D. |
B
解析

练习册系列答案
相关题目
甲、乙二人从A地沿同一方向去B地,途中都使用两种不同的速度 与
与 (
( <
< ). 甲前一半的路程使用速度
). 甲前一半的路程使用速度 ,后一半的路程使用速度
,后一半的路程使用速度 ;乙前一半的时间使用速度
;乙前一半的时间使用速度 ,后一半时间使用速度
,后一半时间使用速度 .关于甲、乙二人从A地到达B地的路程与时间的函数图象及关系,有如图所示的四个不同的图示分析(其中横轴
.关于甲、乙二人从A地到达B地的路程与时间的函数图象及关系,有如图所示的四个不同的图示分析(其中横轴 表示时间,纵轴
表示时间,纵轴 表示路程,C是AB的中点),则其中可能正确的图示分析为 ( )
表示路程,C是AB的中点),则其中可能正确的图示分析为 ( )
| A.(1) | B.(2) | C.(3) | D.(4) |
定义在 上的函数
上的函数 满足:
满足:
(1)对任意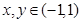 ,都有
,都有 ;
;
(2)对任意 ,都有
,都有 .
.
若 ,
, ,
, ,则
,则 、
、 、
、 的大小关系为( )
的大小关系为( )
A. < < < < | B. < < < < |
C. < < < < | D. < < < < |
函数 的定义域为( )
的定义域为( )
A. | B. | C.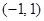 | D. |
已知 是定义在
是定义在 上的函数,其图象是一条连续的曲线,且满足下列条件:
上的函数,其图象是一条连续的曲线,且满足下列条件:
① 的值域为M,且MÍ
的值域为M,且MÍ ;
;
②对任意不相等的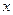 ,
, ∈
∈ , 都有|
, 都有| -
- |<|
|<|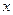 -
- |.
|.
那么,关于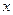 的方程
的方程 =
=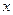 在区间
在区间 上根的情况是 ( )
上根的情况是 ( )
| A.没有实数根 | B.有且仅有一个实数根 |
| C.恰有两个不等的实数根 | D.实数根的个数无法确定 |
函数y= 的值域是[-2,2],则函数y=
的值域是[-2,2],则函数y= 的值域是(▲)
的值域是(▲)
| A.[-2,2] | B.[-4,0] | C.[0,4] | D.[-1,1] |
设 为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则
为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则 的解集为 ( )
的解集为 ( )
| A.(-1, 0)∪(2, +∞) | B.(-∞, -2)∪(0, 2 ) |
| C.(-∞, -2)∪(2, +∞) | D.(-2, 0)∪(0, 2 ) |
若对于任意实数 ,都有
,都有 ,且
,且 在(-∞,0]上是增函数,则( )
在(-∞,0]上是增函数,则( )
A. | B. |
C. | D. |
设函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, 单调递减,若数列
单调递减,若数列 是等差数列,且
是等差数列,且 ,则
,则 的值( )
的值( )
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |