题目内容
设F为抛物线y2=4x的焦点,A、B为该抛物线上两点,若| FA |
| FB |
| 0 |
| FA |
| FB |
分析:先过A,B两点分别作准线的垂线,再过B作AC的垂线,垂足为E,如图,在直角三角形ABE中,求得cos∠BAE=
=
得出直线AB的斜率,进而得到直线AB的方程为:y=2
(x-1),将其代入抛物线的方程求得A,B的坐标,最后利用距离公式求得结果即可.
| AE |
| AB |
| 1 |
| 3 |
得出直线AB的斜率,进而得到直线AB的方程为:y=2
| 2 |
解答: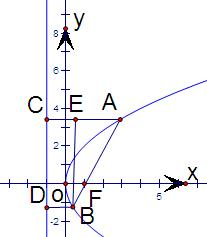 解:过A,B两点分别作准线的垂线,再过B作AC的垂线,垂足为E,
解:过A,B两点分别作准线的垂线,再过B作AC的垂线,垂足为E,
设BF=m,则BD=m,
∵
+2
=
,
∴AC=AF=2m,
如图,在直角三角形ABE中,
AE=AC-BD=2m-m=m,
AB=3m,∴cos∠BAE=
=
∴直线AB的斜率为:k=tan∠BAE=2
∴直线AB的方程为:y=2
(x-1)
将其代入抛物线的方程化简得:2x2-5x+2=0
∴x1=2,x2=
∴A(2,2
).B(
,
),又F(1,0)
则|
|+2|
|=2
=6.
故答案为:6.
 解:过A,B两点分别作准线的垂线,再过B作AC的垂线,垂足为E,
解:过A,B两点分别作准线的垂线,再过B作AC的垂线,垂足为E,设BF=m,则BD=m,
∵
| FA |
| FB |
| 0 |
∴AC=AF=2m,
如图,在直角三角形ABE中,
AE=AC-BD=2m-m=m,
AB=3m,∴cos∠BAE=
| AE |
| AB |
| 1 |
| 3 |
∴直线AB的斜率为:k=tan∠BAE=2
| 2 |
∴直线AB的方程为:y=2
| 2 |
将其代入抛物线的方程化简得:2x2-5x+2=0
∴x1=2,x2=
| 1 |
| 2 |
∴A(2,2
| 2 |
| 1 |
| 2 |
| 2 |
则|
| FA |
| FB |
| 1+8 |
故答案为:6.
点评:本题主要考查了抛物线的简单性质、共线向量及解三角形的知识,解答本题的关键是利用抛物线的定义作出直角三角形ABE,从而求得直线的斜率,体现了数形结合起来的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目