题目内容

已知f（x）=sin(ωx+
π
3
)（ω＞0），f（
π
6
）=f（
π
3
），且f（x）在区间(
π
6
，
π
3
)上有最小值，无最大值，则ω=
 
．
分析：根据f（
π
6
）=f（
π
3
），且f（x）在区间(
π
6
，
π
3
)上有最小值，无最大值，确定最小值时的x值，然后确定ω的表达式，进而推出ω的值．
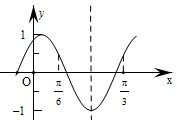解答：精英家教网解：如图所示，
∵f（x）=sin(ωx+
π
3
)，
且f（
π
6
）=f（
π
3
），
又f（x）在区间(
π
6
，
π
3
)内只有最小值、无最大值，
∴f（x）在
π
6
+
π
3
2
=
π
4
处取得最小值．
∴
π
4
ω+
π
3
=2kπ-
π
2
（k∈Z）．
∴ω=8k-
10
3
（k∈Z）．
∵ω＞0，
∴当k=1时，ω=8-
10
3
=
14
3
；
当k=2时，ω=16-
10
3
=
38
3
，此时在区间(
π
6
，
π
3
)内已存在最大值．
故ω=
14
3
．
故答案为：
14
3
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查逻辑思维能力，分析判断能力，是基础题．
练习册系列答案
相关题目
已知f（x）=sin（x+
π
2
），g（x）=cos（x-
π
2
），则f（x）的图象（　　）
A、与g（x）的图象相同
B、与g（x）的图象关于y轴对称
C、向左平移
π
2
个单位，得到g（x）的图象
D、向右平移
π
2
个单位，得到g（x）的图象
已知f（x）=
sinπx   (x＜0)
f(x-1)-1 (x＞0)
，则f（-
11
6
）+f（
11
6
）=
-2
-2
．
已知f（x）=sin（ωx+
π
3
）（ω＞0）的图象与y=-1的图象的相邻两交点间的距离为π，要得到y=f（x）的图象，只需把y=cos2x的图象（　　）
已知f（x）=sin（x+
π
2
），g（x）=cos（x-
π
2
），则f（x）的图象（　　）
已知f（x）=sinπx．
（1）设g(x)=
f(x)，(x≥0)
g(x+1)+1，(x＜0)
，求g(
1
4
)和g(-
1
3
)；
（2）设h(x)=f2(x)+
3
f(x)cosπx+1，求h（x）的最大值及此时x值的集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网