题目内容
如图1,△ABC的三边长分别为AC=6、AB=8、BC=10,O′为其内心;取O′A、O′B、O′C的中点A′、B′、C′,并按虚线剪拼成一个直三棱柱ABC-A′B′C′(如图2),上下底面的内心分别为O′与O;
 (Ⅰ)求直三棱柱ABC-A′B′C′的体积;
(Ⅰ)求直三棱柱ABC-A′B′C′的体积;
(Ⅱ)直三棱柱ABC-A′B′C′中,设线段OO'与平面AB′C交于点P,求二面角B-AP-C的余弦值.
 (Ⅰ)求直三棱柱ABC-A′B′C′的体积;
(Ⅰ)求直三棱柱ABC-A′B′C′的体积;(Ⅱ)直三棱柱ABC-A′B′C′中,设线段OO'与平面AB′C交于点P,求二面角B-AP-C的余弦值.
分析:(I)根据△ABC的三边的平方关系,得△ABC为直角三角形,算出其内切圆半径r=2,从而得到直三棱柱ABC-A′B′C′的底面三角形的形状和高AA'的长,结合柱体体积公式即可算出直三棱柱ABC-A′B′C′的体积;
(II)以A为原点,AB、AC、AA'为x轴、y轴、z轴建立空间直角坐标系,可得向量
、
坐标,利用垂直向量数量积为零的方法建立方程组,解出
=(1,0,-4)是平面AB'C的一个法向量;同样的方法算出
=(0,1,-4)是平面ABP的一个法向量,利用空间向量的夹角公式算出cos<
,
>=
,结合图形加以观察即可得到二面角B-AP-C的余弦值.
(II)以A为原点,AB、AC、AA'为x轴、y轴、z轴建立空间直角坐标系,可得向量
| AB′ |
| AP |
| m |
| n |
| m |
| n |
| 16 |
| 17 |
解答: 解:(Ⅰ)根据题意,可得△ABC为直角三角形,
解:(Ⅰ)根据题意,可得△ABC为直角三角形,
∵△ABC的内切圆半径r=
=2,-----(1分)
∴直三棱柱ABC-A'B'C'的高等于
r=1,-----------------------------(2分)
∵△A'B'C'是两条直角边分别为3、4的直角三角形,
∴直三棱柱ABC-A′B′C′的体积V=(
×3×4)×1=6;-----------(5分)
(Ⅱ)如图,以A为原点,AB、AC、AA'为x轴、y轴、z轴建立空间直角坐标系,
则
=(4,0,1),
=(0,3,0),
设平面AB'C的法向量
=(x,y,z),
则
,取x=1,得y=0,z=-4,所以
=(1,0,-4)--------------------(7分)
再设
=(1,1,z0),由
•
=0算出z0=
,可得
=(1,1,
);-------------(10分)
而
=(4,0,0),设平面ABP的法向量
=(x′,y′,z′),
则
,取y'=1,可得
=(0,1,-4);-------------------------------(12分)
∴cos<
,
>=
=
,
再根据图形,得二面角B-AP-C为钝角,即二面角B-AP-C的平面角与<
,
>互为补角
因此,二面角B-AP-C的余弦值等于-
.------------------------------------(14分)
 解:(Ⅰ)根据题意,可得△ABC为直角三角形,
解:(Ⅰ)根据题意,可得△ABC为直角三角形,∵△ABC的内切圆半径r=
| 6+8-10 |
| 2 |
∴直三棱柱ABC-A'B'C'的高等于
| 1 |
| 2 |
∵△A'B'C'是两条直角边分别为3、4的直角三角形,
∴直三棱柱ABC-A′B′C′的体积V=(
| 1 |
| 2 |
(Ⅱ)如图,以A为原点,AB、AC、AA'为x轴、y轴、z轴建立空间直角坐标系,
则
| AB′ |
| AC |
设平面AB'C的法向量
| m |
则
|
| m |
再设
| AP |
| AP |
| m |
| 1 |
| 4 |
| AP |
| 1 |
| 4 |
而
| AB |
| n |
则
|
| n |
∴cos<
| m |
| n |
| 1×0+0×1+(-4)×(-4) | ||||
|
| 16 |
| 17 |
再根据图形,得二面角B-AP-C为钝角,即二面角B-AP-C的平面角与<
| m |
| n |
因此,二面角B-AP-C的余弦值等于-
| 16 |
| 17 |
点评:本题给出直角三角形的折叠问题,求折成的三棱柱的体积并求二面角的余弦值,着重考查了直角三角形内切圆的性质、柱体体积的求法和利用空间向量求二面角大小等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
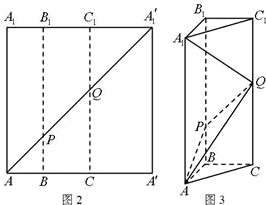 如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.
如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.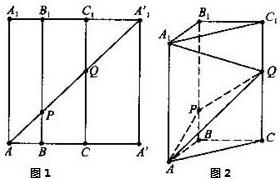 如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,请在图2中解决下列问题:
如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,请在图2中解决下列问题: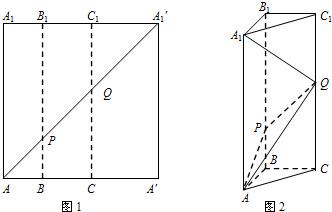 如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.