题目内容
设x,y∈R, 、
、 ,为直角坐标平面内x轴,y轴正方向上的单位向量,若向量
,为直角坐标平面内x轴,y轴正方向上的单位向量,若向量 =x
=x +(y+2)
+(y+2) ,
,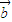 =x
=x +(y-2)
+(y-2) ,且|
,且| |+|
|+| |=8.
|=8.(1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A、B两点.设
 =
= +
+ ,是否存在这样的直线l,使得四边形OAPB为菱形?若存在,求出直线l的方程;若不存在,请说明理由.
,是否存在这样的直线l,使得四边形OAPB为菱形?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】分析:(1)根据向量模的公式以及坐标系内两点间的距离公式,可得动点M(x,y)到定点F1(0,-2)、F2(0,2)的距离之和等于8(常数),由此结合椭圆的定义得到M的轨迹是以F1、F2为焦点的椭圆,可得轨迹C的方程;
(2)设A(x1,y1),B(x2,y2),直线l方程为y=kx+3,将l方程与椭圆C消去y得关于x的方程,得关于x的一元二次方程,利用根与系数的关系及直线l方程得x1+x2=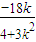 且y1+y2=
且y1+y2=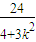 .再根据平行四边形OAPB为菱形,得到|
.再根据平行四边形OAPB为菱形,得到|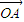 |=|
|=|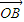 |,利用向量模的公式化简结合前面的等式可得关于k的方程,解之得k=0.由此可得存在直线y=3使得四边形OAPB为菱形.
|,利用向量模的公式化简结合前面的等式可得关于k的方程,解之得k=0.由此可得存在直线y=3使得四边形OAPB为菱形.
解答:解:(1)∵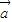 =x
=x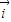 +(y+2)
+(y+2)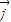 ,
,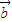 =x
=x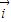 +(y-2)
+(y-2)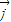
∴|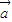 |=
|= ,|
,|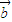 |=
|=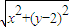
设F1(0,-2),F2(0,2),动点M(x,y),可得|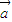 |、|
|、|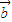 |分别表示点M到F1、F2的距离.
|分别表示点M到F1、F2的距离.
∵|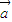 |+|
|+|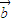 |=8,即M到F1、F2的距离之和等于8,
|=8,即M到F1、F2的距离之和等于8,
∴点M(x,y)的轨迹C是以F1(0,-2),F2(0,2)为焦点,长轴长为8的椭圆,
可得a=4,c=2,b2=a2-c2=12,
可得椭圆方程为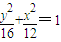 ,即为点M(x,y)的轨迹C的方程;
,即为点M(x,y)的轨迹C的方程;
(2)由于直线l过点(0,3),故
①当直线l为y轴时,A、B为椭圆的顶点,可得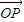 =
=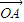 +
+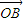 =
=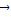
此时点P与原点重合,不符合题意;
②当直线l与x轴不垂直时,设方程为y=kx+3,A(x1,y1),B(x2,y2)
由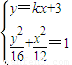 消去y,得(4+3k2)x2+18kx-21=0
消去y,得(4+3k2)x2+18kx-21=0
此时△=(18k)2-4(4+3k2)•(-21)=576k2+336>0恒成立
x1+x2=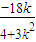 ,代入直线得y1+y2=k(x1+x2)+6=
,代入直线得y1+y2=k(x1+x2)+6=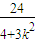
∵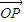 =
=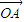 +
+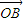 ,∴四边形OAPB是平行四边形,
,∴四边形OAPB是平行四边形,
若四边形OAPB是菱形,则|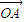 |=|
|=|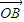 |
|
∵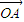 =(x1,y1),
=(x1,y1),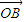 =(x2,y2)
=(x2,y2)
∴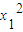 +
+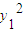 =
=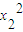 +
+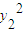 ,化简得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0
,化简得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0
可得l的斜率k=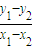 =-
=-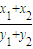 =-
=-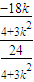 =-
=-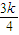
解之得k=0,因此存在直线y=3,使得四边形OAPB为菱形.
点评:本题给出向量关系式,求动点M的轨迹方程并讨论菱形OAPB的存在性.着重考查了向量的坐标运算、椭圆的定义与标准方程和直线与圆锥曲线的位置关系等知识,属于中档题.
(2)设A(x1,y1),B(x2,y2),直线l方程为y=kx+3,将l方程与椭圆C消去y得关于x的方程,得关于x的一元二次方程,利用根与系数的关系及直线l方程得x1+x2=
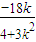 且y1+y2=
且y1+y2=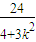 .再根据平行四边形OAPB为菱形,得到|
.再根据平行四边形OAPB为菱形,得到|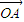 |=|
|=|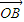 |,利用向量模的公式化简结合前面的等式可得关于k的方程,解之得k=0.由此可得存在直线y=3使得四边形OAPB为菱形.
|,利用向量模的公式化简结合前面的等式可得关于k的方程,解之得k=0.由此可得存在直线y=3使得四边形OAPB为菱形.解答:解:(1)∵
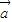 =x
=x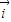 +(y+2)
+(y+2)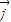 ,
,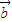 =x
=x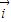 +(y-2)
+(y-2)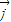
∴|
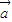 |=
|= ,|
,|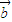 |=
|=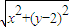
设F1(0,-2),F2(0,2),动点M(x,y),可得|
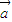 |、|
|、|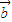 |分别表示点M到F1、F2的距离.
|分别表示点M到F1、F2的距离.∵|
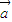 |+|
|+|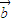 |=8,即M到F1、F2的距离之和等于8,
|=8,即M到F1、F2的距离之和等于8,∴点M(x,y)的轨迹C是以F1(0,-2),F2(0,2)为焦点,长轴长为8的椭圆,
可得a=4,c=2,b2=a2-c2=12,
可得椭圆方程为
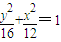 ,即为点M(x,y)的轨迹C的方程;
,即为点M(x,y)的轨迹C的方程;(2)由于直线l过点(0,3),故
①当直线l为y轴时,A、B为椭圆的顶点,可得
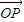 =
=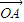 +
+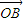 =
=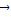
此时点P与原点重合,不符合题意;
②当直线l与x轴不垂直时,设方程为y=kx+3,A(x1,y1),B(x2,y2)
由
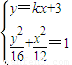 消去y,得(4+3k2)x2+18kx-21=0
消去y,得(4+3k2)x2+18kx-21=0此时△=(18k)2-4(4+3k2)•(-21)=576k2+336>0恒成立
x1+x2=
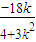 ,代入直线得y1+y2=k(x1+x2)+6=
,代入直线得y1+y2=k(x1+x2)+6=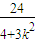
∵
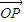 =
=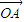 +
+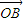 ,∴四边形OAPB是平行四边形,
,∴四边形OAPB是平行四边形,若四边形OAPB是菱形,则|
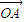 |=|
|=|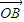 |
|∵
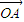 =(x1,y1),
=(x1,y1),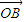 =(x2,y2)
=(x2,y2)∴
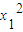 +
+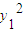 =
=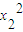 +
+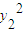 ,化简得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0
,化简得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0可得l的斜率k=
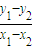 =-
=-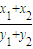 =-
=-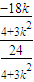 =-
=-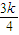
解之得k=0,因此存在直线y=3,使得四边形OAPB为菱形.
点评:本题给出向量关系式,求动点M的轨迹方程并讨论菱形OAPB的存在性.着重考查了向量的坐标运算、椭圆的定义与标准方程和直线与圆锥曲线的位置关系等知识,属于中档题.

练习册系列答案
相关题目