Question

已知O为坐标原点,圆x²+y²+x-6y+C=0与直线x+2y-3=0的两交点为P、Q,当C为何值时OP⊥OQ?

Answer 1

思路分析:设P(x₁,y₁)、Q(x₂,y₂).由OP⊥OQx₁x₂+y₁y₂=0.

由方程组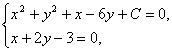解得x₁、x₂、y₁、y₂.代入上式即可求C.

解法一:如图.设P(x₁,y₁)、Q(x₂,y₂).

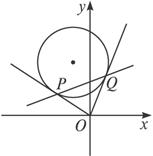
∵OP⊥OQ,

∴k_OP·k_OQ=-1.

∴x₁x₂+y₂y₂=0.                                                                 ①

由方程组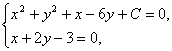消去x得到5y²-20y+12+C=0,

∴y₁+y₂=4,y₁y₂=.

∴x₁x₂=(3-2y₁)(3-2y₂)=9-6(y₁+y₂)+4y₁y₂.

∴x₁x₂+y₁y₂=5y₁y₂-6(y₁+y₂)+9=0,

即12+C-6×4+9=0,解得C=3.

解法二:∵OP⊥OQ,

∴O、P、Q三点共圆,PQ是直径.

故以PQ为直径的圆的圆心为(m,n),方程为(x-m)²+(y-n)²=m²+n².

PQ为两圆的公共弦.两圆相减得PQ方程为(1+2m)x+(-6+2n)y+C=0,它与直线x+2y-3=0是同一直线,

∴，m=-,n=-.

∵圆心(m,n)在直线x+2y-3=0上,

∴--3=0.

∴C=3.