题目内容
(本题满分14分)
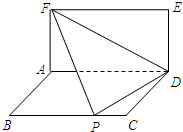
如图,在直三棱柱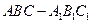 中,
中,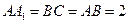 ,
,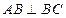 ,求二面角
,求二面角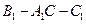 的大小.
的大小.
如图,在直三棱柱
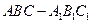 中,
中,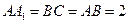 ,
,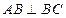 ,求二面角
,求二面角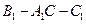 的大小.
的大小.方法1(坐标法)如图,建立空间直角坐标系,则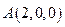 ,
,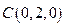 ,
,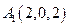 ,
,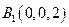 ,
,
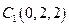 , ……2分
, ……2分
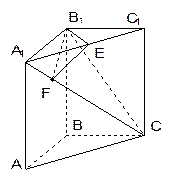
设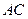 的中点为
的中点为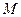 ,因为
,因为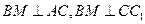 ,所以
,所以 即
即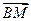 =
=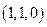 是平面
是平面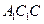 的一个法向量. ……5分
的一个法向量. ……5分
设平面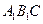 的一个法向量是
的一个法向量是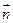 =
=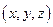 .
.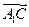 =
=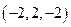 ,
,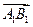 =
=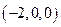 .……7分
.……7分
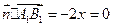 ,
, 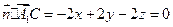 ,令
,令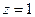 ,解得
,解得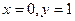 所以
所以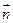 =
=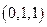
设法向量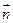 与
与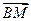 的夹角为
的夹角为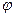 ,二面角
,二面角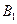 -
-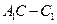 的大小为
的大小为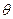 ,显然
,显然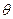 为锐角.
为锐角.
因为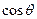 =
=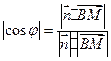 =
=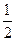 ,解得
,解得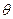 =
=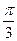 .所以二面角
.所以二面角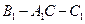 的大小为
的大小为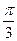 ……14分.
……14分.
方法2(传统法)取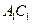 中点
中点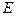 ,做
,做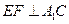 交于
交于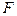 点,因为
点,因为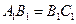 ,所以
,所以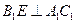 ,
,
在直棱柱中,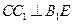 ,所以
,所以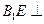 面
面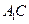 .因为
.因为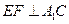 ,由三垂线定理,所以
,由三垂线定理,所以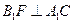 则
则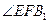 就是所求.
就是所求.
由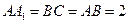 可求:
可求: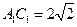 ,
,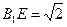 ,
,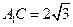 ,由
,由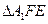 和
和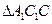 相似可得
相似可得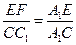 ,可求
,可求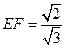 ,
,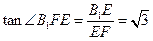 ,所以
,所以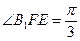
即二面角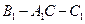 的大小为
的大小为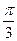 .
.
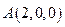 ,
,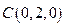 ,
,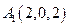 ,
,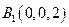 ,
,
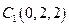 , ……2分
, ……2分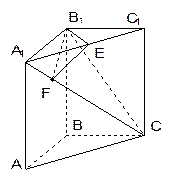
设
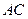 的中点为
的中点为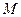 ,因为
,因为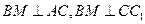 ,所以
,所以 即
即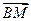 =
=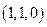 是平面
是平面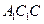 的一个法向量. ……5分
的一个法向量. ……5分设平面
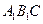 的一个法向量是
的一个法向量是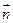 =
=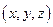 .
.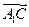 =
=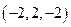 ,
,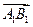 =
=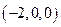 .……7分
.……7分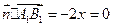 ,
, 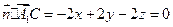 ,令
,令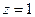 ,解得
,解得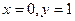 所以
所以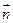 =
=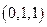
设法向量
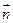 与
与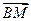 的夹角为
的夹角为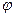 ,二面角
,二面角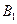 -
-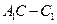 的大小为
的大小为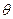 ,显然
,显然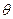 为锐角.
为锐角.因为
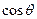 =
=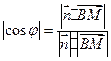 =
=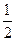 ,解得
,解得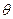 =
=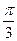 .所以二面角
.所以二面角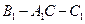 的大小为
的大小为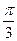 ……14分.
……14分.
方法2(传统法)取
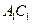 中点
中点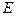 ,做
,做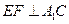 交于
交于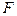 点,因为
点,因为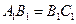 ,所以
,所以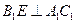 ,
,在直棱柱中,
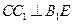 ,所以
,所以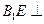 面
面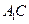 .因为
.因为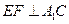 ,由三垂线定理,所以
,由三垂线定理,所以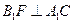 则
则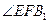 就是所求.
就是所求.由
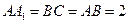 可求:
可求: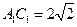 ,
,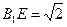 ,
,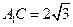 ,由
,由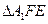 和
和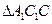 相似可得
相似可得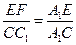 ,可求
,可求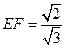 ,
,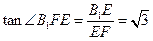 ,所以
,所以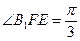
即二面角
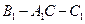 的大小为
的大小为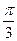 .
. 从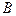 出发的三条棱互相垂直,可以建立直角坐标系,利用向量法解决,计算量较大.因为垂直关系比较明显,所以也可以采用传统的方法,先做出二面角的平面角,再证明,最后求出来.
出发的三条棱互相垂直,可以建立直角坐标系,利用向量法解决,计算量较大.因为垂直关系比较明显,所以也可以采用传统的方法,先做出二面角的平面角,再证明,最后求出来.

 出发的三条棱互相垂直,可以建立直角坐标系,利用向量法解决,计算量较大.因为垂直关系比较明显,所以也可以采用传统的方法,先做出二面角的平面角,再证明,最后求出来.
出发的三条棱互相垂直,可以建立直角坐标系,利用向量法解决,计算量较大.因为垂直关系比较明显,所以也可以采用传统的方法,先做出二面角的平面角,再证明,最后求出来.

练习册系列答案
相关题目
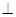 BD B
BD B  为等边三角形
为等边三角形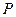 是平面
是平面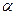 外一点,则下列命题正确的是
外一点,则下列命题正确的是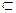 α, 则n
α, 则n