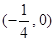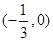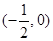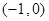题目内容
设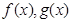 分别是定义在
分别是定义在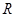 上的奇函数和偶函数,当
上的奇函数和偶函数,当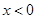 时,
时,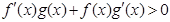 ,
,
且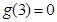 ,则不等式
,则不等式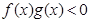 的解集是( )
的解集是( )
A.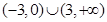 | B.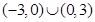 |
C.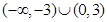 | D.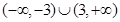 |
C
解析试题分析:令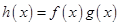 ,当
,当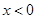 时,
时,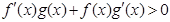 ,即
,即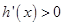 ,
,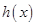 为增函数;
为增函数;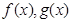 分别是定义在
分别是定义在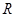 上的奇函数和偶函数,
上的奇函数和偶函数,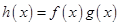 为奇函数,那么当
为奇函数,那么当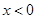 时,
时,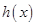 为减函数,又
为减函数,又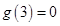 ,所以
,所以 ,可得不等式
,可得不等式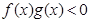 的解集是
的解集是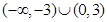 .
.
考点:1.函数的奇偶性;2.导数与函数的单调性的关系.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
若函数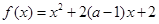 在区间
在区间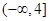 内递减,那么实数
内递减,那么实数 的取值范围为( )
的取值范围为( )
A.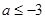 | B.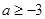 | C.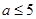 | D.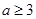 |
设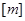 表示不超过实数
表示不超过实数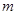 的最大整数,则在直角坐标平面
的最大整数,则在直角坐标平面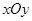 上满足
上满足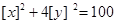 的点
的点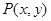 所形成的图形的面积为( )
所形成的图形的面积为( )
| A.10 | B.12 | C.10 | D.12 |
函数f(x)=xe-x,x∈[0,4]的最大值是( )
| A.0 | B. | C.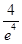 | D.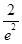 |
设函数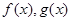 的定义域为
的定义域为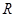 ,且
,且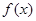 是奇函数,
是奇函数,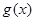 是偶函数,则下列结论中正确的是
是偶函数,则下列结论中正确的是
A.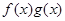 是偶函数 是偶函数 | B.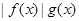 是奇函数 是奇函数 |
C.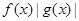 是奇函数 是奇函数 | D.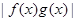 是奇函数 是奇函数 |
设函数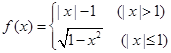 关于
关于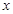 的方程
的方程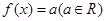 的解的个数不可能是( )
的解的个数不可能是( )
| A.1 | B.2 | C.3 | D.4 |
函数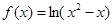 的定义域为( )
的定义域为( )
A.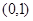 | B. | C.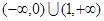 | D. |
直线y=x与函数f(x)= 的图象恰有三个公共点,则实数m的取值范围是( )
的图象恰有三个公共点,则实数m的取值范围是( )
| A.[-1,2) | B.[-1,2] | C.[2,+∞) | D.(-∞,-1] |
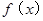 是以
是以 为周期的偶函数,当
为周期的偶函数,当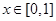 时,
时,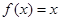 ,那么在区间
,那么在区间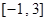 内,关于
内,关于 的方程
的方程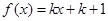 (
(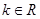 且
且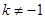 )有
)有 个不同的根,则
个不同的根,则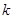 的取值范围是( )
的取值范围是( )