题目内容
不论m取任何实数,直线l:(m-1)x-y+2m+1=0恒过一定点,则该定点的坐标是
- A.(2,3)
- B.(-2,3)
- C.(-2,0)
- D.
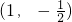
B
分析:直线l:(m-1)x-y+2m+1=0可变形为:m(x+2)+(-x-y+1)=0,根据m∈R,可得方程组,解方程组,即可求得定点的坐标.
解答:直线l:(m-1)x-y+2m+1=0可变形为:m(x+2)+(-x-y+1)=0
∵m∈R
∴
∴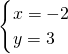
∴不论m取任何实数,直线l:(m-1)x-y+2m+1=0恒过一定点(-2,3)
故选B.
点评:本题重点考查直线恒过定点问题,将方程恰当变形,构建方程组是解题的关键.
分析:直线l:(m-1)x-y+2m+1=0可变形为:m(x+2)+(-x-y+1)=0,根据m∈R,可得方程组,解方程组,即可求得定点的坐标.
解答:直线l:(m-1)x-y+2m+1=0可变形为:m(x+2)+(-x-y+1)=0
∵m∈R
∴

∴
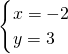
∴不论m取任何实数,直线l:(m-1)x-y+2m+1=0恒过一定点(-2,3)
故选B.
点评:本题重点考查直线恒过定点问题,将方程恰当变形,构建方程组是解题的关键.

练习册系列答案
相关题目
