题目内容
设函数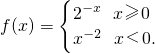
若f（x0）＜1，则x0的取值范围是________．
（-∞，-1）∪（0，+∞）
分析：分x0≥0和x0＜0讨论，x0≥0得
＜1，x0＜0时，得x0-2＜1，分别求解即可．
解答：x0≥0时，f（x0）=＜1?-x0＜0，x0＞0
x0＜0时，f（x0）=x0-2＜1?x02＞1，x0＜-1
综上所述：x0＞0或x0＜-1
故答案为：（-∞，-1）∪（0，+∞）
点评：本题考查分段函数、解不等式等知识，属基本题．
分析：分x0≥0和x0＜0讨论，x0≥0得
＜1，x0＜0时，得x0-2＜1，分别求解即可．解答：x0≥0时，f（x0）=
＜1?-x0＜0，x0＞0x0＜0时，f（x0）=x0-2＜1?x02＞1，x0＜-1
综上所述：x0＞0或x0＜-1
故答案为：（-∞，-1）∪（0，+∞）
点评：本题考查分段函数、解不等式等知识，属基本题．
练习册系列答案
相关题目
若不存在x0∈R，使得f(x0)＜0与g(x0)＜0同时成立，则实数a的取值范围是________．
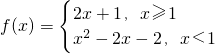若f（x0）＞1，则x0的取值范围为________．
若f（x0） >1，则x0的取值范围是