题目内容
设F1、F2分别为椭圆C: 的左、右两个焦点,椭圆C上一点P(1,
的左、右两个焦点,椭圆C上一点P(1, )到F1、F2两点的距离之和等于4.又直线l:y=
)到F1、F2两点的距离之和等于4.又直线l:y= x+m与椭圆C有两个不同的交点A、B,O为坐标原点.
x+m与椭圆C有两个不同的交点A、B,O为坐标原点.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l经过点F1,求△ABF2的面积;
(Ⅲ)求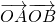 的取值范围.
的取值范围.
解:(Ⅰ)由题设可知,椭圆的焦点在x轴上,且2a=4,即a=2. (1分)
又点A(1, )在椭圆上,∴
)在椭圆上,∴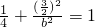 ,解得b2=3.(2分)
,解得b2=3.(2分)
∴椭圆C的标准方程是 . (3分)
. (3分)
(Ⅱ)由(Ⅰ)知,c2=a2-b2=1,即c=1,
∴F1、F2两点的坐标分别为(-1,0)、(1,0). (4分)
∵直线l:y= x+m经过点F1(-1,0),
x+m经过点F1(-1,0),
∴0= ×(-1)+m,∴m=
×(-1)+m,∴m= . (5分)
. (5分)
设A、B两点的坐标分别为(x1,y1)、(x2,y2),由题意,有
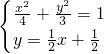 ,消去x,整理得16y2-12y-9=0,
,消去x,整理得16y2-12y-9=0,
∴y1+y2= ,y1y2=-
,y1y2=- . (6分)
. (6分)
设△ABF2的面积为SABF2,则
SABF2= |F1F2||y2-y1|=
|F1F2||y2-y1|= ×2
×2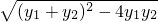 =
=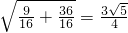
(Ⅲ)设A、B的坐标分别为(x1,y1)、(x2,y2),则由题意,有
 ,消去y,整理得x2+mx+m2-3=0 ①
,消去y,整理得x2+mx+m2-3=0 ①
x1+x2=-m,x1x2=m2-3.
∴y1y2=( x1+m)(
x1+m)( x2+m)=
x2+m)= x1x2+
x1x2+ (x1+x2)m+m2
(x1+x2)m+m2
= (m2-3)+
(m2-3)+ (-m)m+m2=
(-m)m+m2= m2-
m2- . (10分)
. (10分)
∴ =x1x2+y1y2=m2-3+
=x1x2+y1y2=m2-3+ m2-
m2- =
= m2-
m2- ,(11分)
,(11分)
又由①得,△=m2-4(m2-3)=-3m2+12,
∵A、B为不同的点,∴△>0,∴0≤m2<4.
∴- ≤
≤
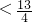 .
.
∴ 的取值范围是[-
的取值范围是[- ,
, ). (14分)
). (14分)
分析:(Ⅰ)由题设可知,椭圆的焦点在x轴上,求出a=2,又点A(1, )在椭圆上,解得b,最后写出椭圆C的标准方程;
)在椭圆上,解得b,最后写出椭圆C的标准方程;
(Ⅱ)由(Ⅰ)知,F1、F2两点的坐标;直线l:y= x+m经过点F1求得m,设A、B两点的坐标分别为(x1,y1)、(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△ABF2的面积,从而解决问题.
x+m经过点F1求得m,设A、B两点的坐标分别为(x1,y1)、(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△ABF2的面积,从而解决问题.
(Ⅲ)设A、B的坐标分别为(x1,y1)、(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的数量积坐标公式即可求得求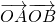 的取值范围.
的取值范围.
点评:本小题主要考查椭圆的标准方程、平面向量数量积的运算、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查方程思想、化归与转化思想.属于基础题.
又点A(1,
 )在椭圆上,∴
)在椭圆上,∴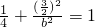 ,解得b2=3.(2分)
,解得b2=3.(2分)∴椭圆C的标准方程是
 . (3分)
. (3分)(Ⅱ)由(Ⅰ)知,c2=a2-b2=1,即c=1,
∴F1、F2两点的坐标分别为(-1,0)、(1,0). (4分)
∵直线l:y=
 x+m经过点F1(-1,0),
x+m经过点F1(-1,0),∴0=
 ×(-1)+m,∴m=
×(-1)+m,∴m= . (5分)
. (5分)设A、B两点的坐标分别为(x1,y1)、(x2,y2),由题意,有
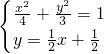 ,消去x,整理得16y2-12y-9=0,
,消去x,整理得16y2-12y-9=0,∴y1+y2=
 ,y1y2=-
,y1y2=- . (6分)
. (6分)设△ABF2的面积为SABF2,则
SABF2=
 |F1F2||y2-y1|=
|F1F2||y2-y1|= ×2
×2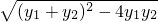 =
=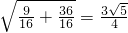
(Ⅲ)设A、B的坐标分别为(x1,y1)、(x2,y2),则由题意,有
 ,消去y,整理得x2+mx+m2-3=0 ①
,消去y,整理得x2+mx+m2-3=0 ①x1+x2=-m,x1x2=m2-3.
∴y1y2=(
 x1+m)(
x1+m)( x2+m)=
x2+m)= x1x2+
x1x2+ (x1+x2)m+m2
(x1+x2)m+m2=
 (m2-3)+
(m2-3)+ (-m)m+m2=
(-m)m+m2= m2-
m2- . (10分)
. (10分)∴
 =x1x2+y1y2=m2-3+
=x1x2+y1y2=m2-3+ m2-
m2- =
= m2-
m2- ,(11分)
,(11分)又由①得,△=m2-4(m2-3)=-3m2+12,
∵A、B为不同的点,∴△>0,∴0≤m2<4.
∴-
 ≤
≤
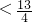 .
.∴
 的取值范围是[-
的取值范围是[- ,
, ). (14分)
). (14分)分析:(Ⅰ)由题设可知,椭圆的焦点在x轴上,求出a=2,又点A(1,
 )在椭圆上,解得b,最后写出椭圆C的标准方程;
)在椭圆上,解得b,最后写出椭圆C的标准方程;(Ⅱ)由(Ⅰ)知,F1、F2两点的坐标;直线l:y=
 x+m经过点F1求得m,设A、B两点的坐标分别为(x1,y1)、(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△ABF2的面积,从而解决问题.
x+m经过点F1求得m,设A、B两点的坐标分别为(x1,y1)、(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△ABF2的面积,从而解决问题.(Ⅲ)设A、B的坐标分别为(x1,y1)、(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的数量积坐标公式即可求得求
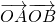 的取值范围.
的取值范围.点评:本小题主要考查椭圆的标准方程、平面向量数量积的运算、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查方程思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点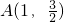 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.