题目内容
设F1,F2分别为椭C: (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点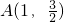 到两点的距离之和等于4.
到两点的距离之和等于4.
(Ⅰ)求椭圆C的方程和焦点坐标;
(Ⅱ)设点P是(Ⅰ)中所得椭圆上的动点 求|PQ|的最大值.
求|PQ|的最大值.
解:(Ⅰ)∵椭圆C上的点A(1, )到椭圆
)到椭圆 +
+ =1(a>b>0)两焦点F1,F2的距离之和等于4,
=1(a>b>0)两焦点F1,F2的距离之和等于4,
∴2a=4,a=2.
∴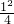 +
+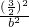 =1,
=1,
∴b2=3,
∴椭圆的方程为: +
+ =1,其焦点坐标为F1(-1,0),F2(1,0);
=1,其焦点坐标为F1(-1,0),F2(1,0);
(Ⅱ)设P(2cosθ, sinθ),
sinθ),
∵Q(0, ),
),
∴|PQ|2=4cos2θ+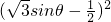
=4-4sin2θ+3sin2θ- sinθ+
sinθ+
=-sin2θ- sinθ+
sinθ+
=-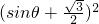 +5≤5.
+5≤5.
∴|PQ|的最大值为 .
.
分析:(Ⅰ)依题意可求得a=2,b2=3,从而可求得椭圆C的方程和焦点坐标;
(Ⅱ)利用椭圆的参数方程,利用配方法与正弦函数的性质即可求得|PQ|的最大值.
点评:本题考查椭圆的标准方程与性质,考查椭圆的参数方程及两点间的距离,考查配方法与最值问题,属于难题.
 )到椭圆
)到椭圆 +
+ =1(a>b>0)两焦点F1,F2的距离之和等于4,
=1(a>b>0)两焦点F1,F2的距离之和等于4,∴2a=4,a=2.
∴
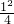 +
+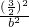 =1,
=1,∴b2=3,
∴椭圆的方程为:
 +
+ =1,其焦点坐标为F1(-1,0),F2(1,0);
=1,其焦点坐标为F1(-1,0),F2(1,0);(Ⅱ)设P(2cosθ,
 sinθ),
sinθ),∵Q(0,
 ),
),∴|PQ|2=4cos2θ+
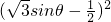
=4-4sin2θ+3sin2θ-
 sinθ+
sinθ+
=-sin2θ-
 sinθ+
sinθ+
=-
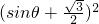 +5≤5.
+5≤5.∴|PQ|的最大值为
 .
.分析:(Ⅰ)依题意可求得a=2,b2=3,从而可求得椭圆C的方程和焦点坐标;
(Ⅱ)利用椭圆的参数方程,利用配方法与正弦函数的性质即可求得|PQ|的最大值.
点评:本题考查椭圆的标准方程与性质,考查椭圆的参数方程及两点间的距离,考查配方法与最值问题,属于难题.

练习册系列答案
相关题目