题目内容
(本小题12分) a,b,c为△ABC的三边,其面积S△ABC=12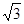 ,bc=48,b-c=2,求a;
,bc=48,b-c=2,求a;
当A=60°时,a2=52,a=2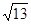 ,当A=120°时,a2=148,a=2
,当A=120°时,a2=148,a=2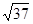 。
。
解析试题分析:利用三角形的面积公式列出关于sinA的等式,求出sinA的值,通过解已知条件中关于b,c的方程求出b,c的值,分两种情况,利用余弦定理求出边a的值.
解:由S△ABC=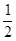 bcsinA,得12
bcsinA,得12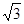 =
=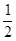 ×48×sinA
×48×sinA
∴ sinA=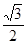 2分
2分
∴ A=60°或A=120° 2分
a2=b2+c2-2bccosA
=(b-c)2+2bc(1-cosA)
=4+2×48×(1-cosA) 4分
当A=60°时,a2=52,a=2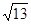 2分
2分
当A=120°时,a2=148,a=2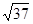 2分
2分
考点:本题主要考查运用正弦面积公式和余弦定理解三角形问题。
点评:解决该试题的关键是求三角形的题目,一般利用正弦定理、余弦定理及三角形的面积公式列方程解决

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
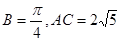 ,
,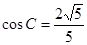 .
.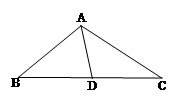
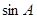 ;
;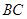 的中点为
的中点为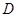 ,求中线
,求中线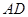 的长.
的长. 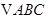 的内角
的内角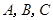 的对边分别是
的对边分别是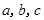 ,且
,且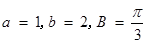 .
.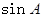 的值; (2) 求
的值; (2) 求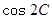 的值.
的值. 的内角
的内角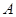 、
、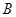 、
、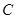 的对边分别为
的对边分别为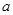 、
、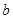 、
、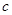 ,已知
,已知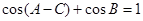 ,
,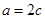 ,求
,求 中,内角
中,内角 的对边分别为
的对边分别为 。若
。若 。(1)证明:
。(1)证明: ;(2)求
;(2)求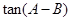 的最大值。
的最大值。 ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=
ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ,sinB=
,sinB= cosC.
cosC. ,求
,求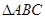 外接圆的半径为2,
外接圆的半径为2,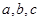 分别是
分别是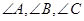 的对边
的对边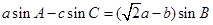
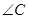 (2)求
(2)求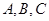 分别是锐角
分别是锐角 的三边
的三边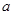 、
、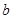 、
、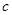 所对的角,
所对的角,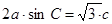 .
. 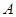 的大小;
的大小;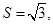 求
求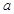 的最小值.
的最小值.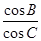 =-
=-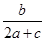 .
. 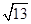 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.