题目内容
下列四个命题:
①p:m<-2或m>6;q:y=x2+mx+m+3有两个不同的零点.
②p: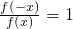 ;q:y=f(x)是偶函数.
;q:y=f(x)是偶函数.
③p:cosα=cosβ;q“tanα=tanβ.
④p:A∩B=A; q:?UB⊆?UA
其中,p是q的充要条件的命题序号是________.
①④
分析:①二次函数f(x)=0有两个不同的零点?△>0,解出即可判断出;
②充分理解函数具有奇偶性,其定义域关于原点对称,即可判断出;
③举出反例即可;
④利用集合间的关系即可判断出.
解答:①q:y=x2+mx+m+3有两个不同的零点?△=m2-4(m+3)>0?m<-2或m>6.因此p是q的充要条件,故①正确;
②由p: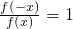 ,可得f(-x)=f(x),但是由f(x)=0解得的解集不一定关于原点对称,故函数y=f(x)不一定是偶函数;
,可得f(-x)=f(x),但是由f(x)=0解得的解集不一定关于原点对称,故函数y=f(x)不一定是偶函数;
反之由q:y=f(x)是偶函数,可能f(x)=0,故不一定有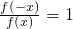 .故p是q的既不充分也不必要条件;
.故p是q的既不充分也不必要条件;
③若 ,则cosα=cosβ,但是tanα与tanβ都不存在;由
,则cosα=cosβ,但是tanα与tanβ都不存在;由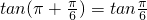 ,但是
,但是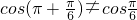 .故p是q的既不充分也不必要条件;
.故p是q的既不充分也不必要条件;
④由A∩B=A,得A⊆B,∴?UB⊆?UA;反之,由?UB⊆?UA,可得A⊆B,∴A∩B=A.故④正确.故p是q的充要条件.
综上可知:p是q的充要条件的命题序号是①④.
故答案为①④.
点评:熟练掌握二次函数的零点与判别式的关系、函数的奇偶性、三角函数的诱导公式及集合间的关系是解题的关键.
分析:①二次函数f(x)=0有两个不同的零点?△>0,解出即可判断出;
②充分理解函数具有奇偶性,其定义域关于原点对称,即可判断出;
③举出反例即可;
④利用集合间的关系即可判断出.
解答:①q:y=x2+mx+m+3有两个不同的零点?△=m2-4(m+3)>0?m<-2或m>6.因此p是q的充要条件,故①正确;
②由p:
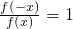 ,可得f(-x)=f(x),但是由f(x)=0解得的解集不一定关于原点对称,故函数y=f(x)不一定是偶函数;
,可得f(-x)=f(x),但是由f(x)=0解得的解集不一定关于原点对称,故函数y=f(x)不一定是偶函数;反之由q:y=f(x)是偶函数,可能f(x)=0,故不一定有
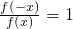 .故p是q的既不充分也不必要条件;
.故p是q的既不充分也不必要条件;③若
 ,则cosα=cosβ,但是tanα与tanβ都不存在;由
,则cosα=cosβ,但是tanα与tanβ都不存在;由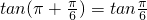 ,但是
,但是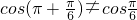 .故p是q的既不充分也不必要条件;
.故p是q的既不充分也不必要条件;④由A∩B=A,得A⊆B,∴?UB⊆?UA;反之,由?UB⊆?UA,可得A⊆B,∴A∩B=A.故④正确.故p是q的充要条件.
综上可知:p是q的充要条件的命题序号是①④.
故答案为①④.
点评:熟练掌握二次函数的零点与判别式的关系、函数的奇偶性、三角函数的诱导公式及集合间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
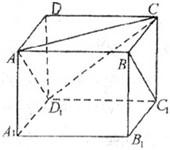 16、如图,正方体ABCD-A1B1C1D1,则下列四个命题:
16、如图,正方体ABCD-A1B1C1D1,则下列四个命题: 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: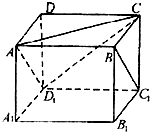 (A题)如图正方体ABCD-A1B1C1D1,则下列四个命题:
(A题)如图正方体ABCD-A1B1C1D1,则下列四个命题: