题目内容
已知向量 与
与  共线,设函数y=f(x).
共线,设函数y=f(x).(1)求函数f(x)的周期及最大值;
(2)已知锐角△ABC中的三个内角分别为A、B、C,若有
 ,边BC=
,边BC= ,
,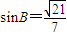 ,求△ABC的面积.
,求△ABC的面积.
【答案】分析:(1)根据向量共线的条件,结合向量 与
与  共线,可求函数f(x)的解析式,从而可求函数的周期与最大值;
共线,可求函数f(x)的解析式,从而可求函数的周期与最大值;
(2)根据 ,可得A=
,可得A= ,利用正弦定理可得AC=2,求出sinC的值,即可求得△ABC的面积.
,利用正弦定理可得AC=2,求出sinC的值,即可求得△ABC的面积.
解答:解:(1)∵向量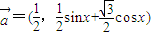 与
与  共线
共线
∴
∴
∴函数f(x)的周期T=2π
当 时,函数f(x)的最大值为2;
时,函数f(x)的最大值为2;
(2)∵
∴
∴
∵
∴A=
∵BC= ,
, ,
,
∴
∴AC=2
∵sinC=sin(π-A-B)=sin(A+B)=sinAcosB+cosAsinB= =
=
∴△ABC的面积S= .
.
点评:本题考查三角函数解析式与性质,考查三角形的面积,解题的关键是利用向量知识,确定函数的解析式.
 与
与  共线,可求函数f(x)的解析式,从而可求函数的周期与最大值;
共线,可求函数f(x)的解析式,从而可求函数的周期与最大值;(2)根据
 ,可得A=
,可得A= ,利用正弦定理可得AC=2,求出sinC的值,即可求得△ABC的面积.
,利用正弦定理可得AC=2,求出sinC的值,即可求得△ABC的面积.解答:解:(1)∵向量
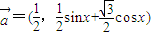 与
与  共线
共线∴

∴

∴函数f(x)的周期T=2π
当
 时,函数f(x)的最大值为2;
时,函数f(x)的最大值为2;(2)∵

∴

∴

∵

∴A=

∵BC=
 ,
, ,
,∴

∴AC=2
∵sinC=sin(π-A-B)=sin(A+B)=sinAcosB+cosAsinB=
 =
=
∴△ABC的面积S=
 .
.点评:本题考查三角函数解析式与性质,考查三角形的面积,解题的关键是利用向量知识,确定函数的解析式.

练习册系列答案
相关题目
 与
与  共线,设函数y=f(x).
共线,设函数y=f(x). ,边BC=
,边BC= ,
, ,求△ABC的面积.
,求△ABC的面积. 与
与  共线,设函数y=f(x).
共线,设函数y=f(x). ,边BC=
,边BC= ,
, ,求△ABC的面积.
,求△ABC的面积. 与
与  共线,设函数y=f(x).
共线,设函数y=f(x). ,边BC=
,边BC= ,
, ,求△ABC的面积.
,求△ABC的面积. 与
与  共线,设函数y=f(x).
共线,设函数y=f(x). ,边BC=
,边BC= ,
, ,求△ABC的面积.
,求△ABC的面积. 与
与  共线,设函数
共线,设函数
 。
。 的周期及最大值;
的周期及最大值; ,边 BC=
,边 BC= ,
, ,求
△ABC 的面积.
,求
△ABC 的面积.