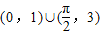题目内容
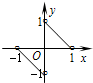 如图,f(x)的定义域为(-1,0)∪(0,1),则不等式f-1(x)-f-1(-x)>-1的解集为( )
如图,f(x)的定义域为(-1,0)∪(0,1),则不等式f-1(x)-f-1(-x)>-1的解集为( )分析:先根据函数f(x)的图象可知该函数为奇函数,则函数f-1(x)也是奇函数,然后化简不等式,再根据原函数与反函数的图象关于直线y=x对称,以及函数f(x)的图象可知函数f-1(x)的图象与之重合,结合图象解不等式即可.
解答:解:根据函数f(x)的图象可知该函数为奇函数,则函数f-1(x)也是奇函数
∴f-1(-x)=-f-1(x)
则f-1(x)-f-1(-x)=2f-1(x)>-1
即f-1(x)>
根据原函数与反函数的图象关于直线y=x对称,以及函数f(x)的图象可知函数f-1(x)的图象与之重合
∴不等式f-1(x)-f-1(-x)>-1的解集为(-1 , -
)∪(0 , 1)
故选D.
∴f-1(-x)=-f-1(x)
则f-1(x)-f-1(-x)=2f-1(x)>-1
即f-1(x)>
| 1 |
| 2 |
根据原函数与反函数的图象关于直线y=x对称,以及函数f(x)的图象可知函数f-1(x)的图象与之重合
∴不等式f-1(x)-f-1(-x)>-1的解集为(-1 , -
| 1 |
| 2 |
故选D.
点评:本题主要考查了反函数,以及原函数与反函数的图象的关系,同时考查了数形结合法解不等式,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
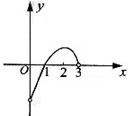 已知f(x)的定义在(0,3)上的函数,f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( )
已知f(x)的定义在(0,3)上的函数,f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( )| A、(0,1)∪(2,3) | ||||
B、(1,
| ||||
C、(0,1)∪(
| ||||
| D、(0,1)∪(1,3) |