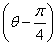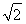题目内容
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B,E,F,C四点共圆.
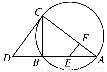
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值.
(1)见解析(2)
【解析】(1)证明:因为CD为△ABC外接圆的切线,
所以∠DCB=∠A.由题设知 ,
,
故△CDB∽△AEF,所以∠DBC=∠EFA.
因为B,E,F,C四点共圆,
所以∠CFE=∠DBC,
故∠EFA=∠CFE=90°,
所以∠CBA=90°.因此CA是△ABC外接圆的直径.
(2)连接CE,因为∠CBE=90°,
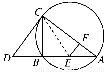
所以过B,E,F,C四点的圆的直径为CE.
由DB=BE,有CE=DC.
又BC2=DB·BA=2DB2,
所以CA2=4DB2+BC2=6DB2.
而CE2=DC2=DB·DA=3DB2,
故过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为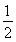 .
.

练习册系列答案
相关题目