题目内容
设f（x）在xo处可导．且f（xo）=0 则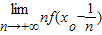
（ ）A．等于f′（xo）
B．等于-f′（xo）
C．等于0
D．不存在
【答案】分析：根据f（xo）=0可将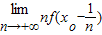
等价变形为
再结合f（x）在xo处可导即可求解．
解答：解∵f（xo）=0
∴
=
∵f（x）在xo处可导
∴
=
=-
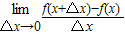=-f′（x）
故选B
点评：本题主要考查极限及其运算．解题的关键是要将题中所述极限转化为为
再根据n→∞时
→0再转化为-
然后再结合f（x）在xo处可导才可求解．此题充分活用了极限和可导的定义，技巧性较强，属中等难度的试题．
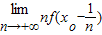等价变形为再结合f（x）在xo处可导即可求解．解答：解∵f（xo）=0
∴
=∵f（x）在xo处可导
∴
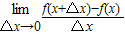==-=-f′（x）故选B
点评：本题主要考查极限及其运算．解题的关键是要将题中所述极限转化为为
再根据n→∞时→0再转化为-然后再结合f（x）在xo处可导才可求解．此题充分活用了极限和可导的定义，技巧性较强，属中等难度的试题． 
练习册系列答案
阅读快车系列答案
相关题目
设f（x）在点x=x0处可导，且
→1(△x→0)，则f′（xo）=（ ）
| f(xo+7△x)-f(xo) |
| △x |
| A、1 | ||
| B、0 | ||
| C、7 | ||
D、
|
