题目内容
设定义在R上的函数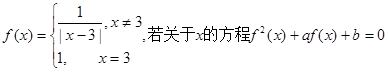 有5个不同实数解,则实数a的取值范围是( )
有5个不同实数解,则实数a的取值范围是( )
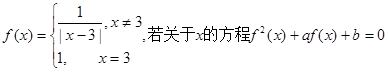 有5个不同实数解,则实数a的取值范围是( )
有5个不同实数解,则实数a的取值范围是( )A.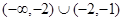 | B.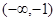 |
C.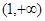 | D.(0,1) |
A
∵题中原方程f2(x)+af(x)+b=0有且只有5个不同实数解,
∴即要求对应于f(x)等于某个常数有3个不同实数解,
∴故先根据题意作出f(x)的简图:
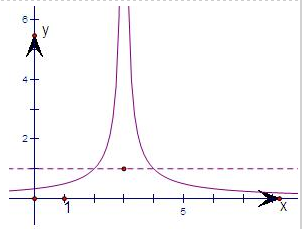
由图可知,只有当f(x)=1时,它有三个根.
故关于x的方程f2(x)+af(x)+b=0中,
有:1+a+b=0,b=-1-a,
且当f(x)=k,k>0且k≠1时,关于x的方程f2(x)+af(x)+b=0有5个不同实数解,
∴k2+ak-1-a=0,
a=-1-k,∵k>0且k≠1,
∴a∈(-∞,-2)∪(-2,-1)
故选A.
∴即要求对应于f(x)等于某个常数有3个不同实数解,
∴故先根据题意作出f(x)的简图:

由图可知,只有当f(x)=1时,它有三个根.
故关于x的方程f2(x)+af(x)+b=0中,
有:1+a+b=0,b=-1-a,
且当f(x)=k,k>0且k≠1时,关于x的方程f2(x)+af(x)+b=0有5个不同实数解,
∴k2+ak-1-a=0,
a=-1-k,∵k>0且k≠1,
∴a∈(-∞,-2)∪(-2,-1)
故选A.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
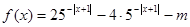 有实数零点,则实数
有实数零点,则实数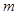 的取值范围是( )
的取值范围是( )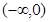
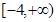
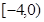
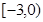
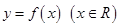 满足
满足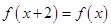 且
且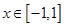 时,
时,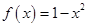 ;函数
;函数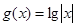 ,则函数
,则函数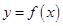 与
与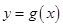 的图象在区间
的图象在区间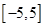 内的交点个数共有 个.
内的交点个数共有 个.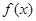 是定义在
是定义在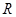 上的奇函数,当
上的奇函数,当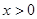 时,
时,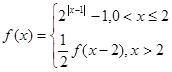 ,则函数
,则函数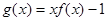 在
在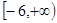 上的所有零点之和等于( )
上的所有零点之和等于( )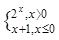 ,若f(a)+f(1)=0,则实数a的值等于 .
,若f(a)+f(1)=0,则实数a的值等于 . ,定义域为D, 若存在
,定义域为D, 若存在 使
使 , 则称
, 则称 为
为 的图象上不动点的坐标为 .
的图象上不动点的坐标为 .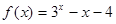 的一个零点,其参考数据如下:
的一个零点,其参考数据如下: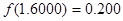





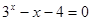 的一个近似解(精确到0.01)为_________.
的一个近似解(精确到0.01)为_________.  的零点个数为
的零点个数为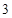 ,则
,则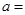 ______.
______. ,若
,若 ,则
,则 的值为__________。
的值为__________。