题目内容
如果实数x,y,t满足|x-t|≤|y-t|,则称x比y接近t.
(1)设a为实数,若a|a| 比a更接近1,求a的取值范围;
(2)f(x)=ln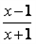 ,证明:
,证明: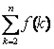 比
比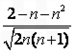 更接近0(k∈Z).
更接近0(k∈Z).
(1)设a为实数,若a|a| 比a更接近1,求a的取值范围;
(2)f(x)=ln
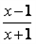 ,证明:
,证明: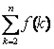 比
比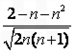 更接近0(k∈Z).
更接近0(k∈Z).(1)解:|a|a|-1|≤|a-1|
①当0<a<1时, |a2-1|≤|a-1|
1-a2≤1-a,得a≥1或a≤0(舍去)
②当a≥1时,a2-1≤a-1, 得a= 1
③当 a≤0时, a2+1≤1-a ,-1≤a≤0 .
综上, a的取值范围是{a|-1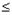 a
a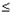 0或a=1}
0或a=1}
(2)证明: ∵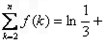
 +
+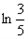 +…+
+…+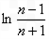 =
=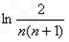 ,
,
∴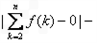
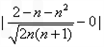 =
=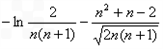 .
.
令n(n+1)=t,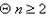
∴t∈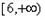 ,且t∈Z,
,且t∈Z,
则F(t)=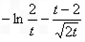 =
=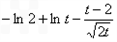 .
.
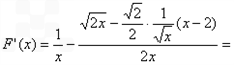
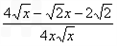 =
=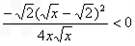
∴F(x)在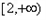 单调递减
单调递减
∴F(t)≤f(6)<F(2)=-ln1-0=0 .
∴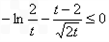
即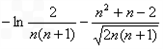 ≤0.
≤0.
∴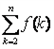 比
比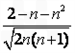 更接近0.
更接近0.
①当0<a<1时, |a2-1|≤|a-1|
1-a2≤1-a,得a≥1或a≤0(舍去)
②当a≥1时,a2-1≤a-1, 得a= 1
③当 a≤0时, a2+1≤1-a ,-1≤a≤0 .
综上, a的取值范围是{a|-1
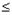 a
a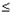 0或a=1}
0或a=1} (2)证明: ∵
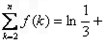
 +
+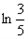 +…+
+…+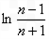 =
=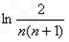 ,
,∴
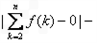
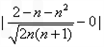 =
=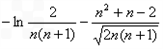 .
.令n(n+1)=t,
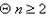
∴t∈
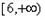 ,且t∈Z,
,且t∈Z,则F(t)=
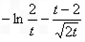 =
=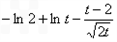 .
.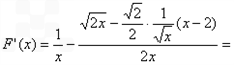
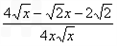 =
=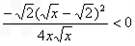
∴F(x)在
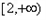 单调递减
单调递减 ∴F(t)≤f(6)<F(2)=-ln1-0=0 .
∴
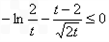
即
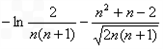 ≤0.
≤0.∴
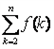 比
比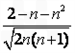 更接近0.
更接近0. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

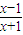 ,证明:
,证明: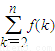 比
比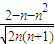 更接近0(k∈Z).
更接近0(k∈Z).