题目内容
如果实数x,y,t满足|x-t|≤|y-t|,则称x比y接近t.
(Ⅰ)设a为实数,若a|a|比a更接近1,求a的取值范围;
(Ⅱ)f(x)=ln
,证明:
f(k)比
更接近0(k∈Z).
(Ⅰ)设a为实数,若a|a|比a更接近1,求a的取值范围;
(Ⅱ)f(x)=ln
| x-1 |
| x+1 |
| n |
 |
| k=2 |
| 2-n-n2 | ||
|
分析:(I)由题意可得,||a|a|-1|≤|a-1|,由于去绝对值需要考虑a的范围,分类讨论:(1)0<a<1(2)a≥1(3)a≤0三种情况求解a的范围
(Ⅱ)要证明
f(k)比
更接近0(k∈Z),只要证明|
f(k)-0|-|
-0|=-ln
-
≤0即可
(Ⅱ)要证明
| n |
 |
| k=2 |
| 2-n-n2 | ||
|
| n |
 |
| k=2 |
| 2-n-n2 | ||
|
| 2 |
| n(n+1) |
| n2+n-2 | ||
|
解答:解:(I)由题意可得,||a|a|-1|≤|a-1|
(1)当0<a<1时,|a2-1|≤|a-1|
1-a2≤1-a,得a≥1或a≤0(舍去)
(2)当a≥1时,a2-1≤a-1,得a=1;
(3)当a≤0时,a2+1≤1-a,-1≤a≤0.
综上,a的取值范围是{a|-1≤a≤0或a=1}
(Ⅱ)∵
f(k)=ln
+ln
+ln
+…+ln
=ln
,
∴|
f(k)-0|-|
-0|=-ln
-
.
令n(n+1)=t,∵n≥2∴t∈[6,+∞),且t∈Z,则
F(t)=-ln
-
=-ln2+lnt-
.F′(x)=
-
=
=
<0
∴F(x)在[2,+∞)单调递减∴F(t)≤f(6)<F(2)=-ln1-0=0.
∴-ln
-
≤0,即-ln
-
≤0.
∴
f(k)比
更接近0.
(1)当0<a<1时,|a2-1|≤|a-1|
1-a2≤1-a,得a≥1或a≤0(舍去)
(2)当a≥1时,a2-1≤a-1,得a=1;
(3)当a≤0时,a2+1≤1-a,-1≤a≤0.
综上,a的取值范围是{a|-1≤a≤0或a=1}
(Ⅱ)∵
| n |
 |
| k=2 |
| 1 |
| 3 |
| 2 |
| 4 |
| 3 |
| 5 |
| n-1 |
| n+1 |
| 2 |
| n(n+1) |
∴|
| n |
 |
| k=2 |
| 2-n-n2 | ||
|
| 2 |
| n(n+1) |
| n2+n-2 | ||
|
令n(n+1)=t,∵n≥2∴t∈[6,+∞),且t∈Z,则
F(t)=-ln
| 2 |
| t |
| t-2 | ||
|
| t-2 | ||
|
| 1 |
| x |
| ||||||||||
| 2x |
4
| ||||||
4x
|
-
| ||||||
4x
|
∴F(x)在[2,+∞)单调递减∴F(t)≤f(6)<F(2)=-ln1-0=0.
∴-ln
| 2 |
| t |
| t-2 | ||
|
| 2 |
| n(n+1) |
| n2+n-2 | ||
|
∴
| n |
 |
| k=2 |
| 2-n-n2 | ||
|
点评:本题以新定义为载体主要考查了绝对值不等式的解法,利用导数判断函数的单调性求解函数的最值,属于综合性试题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
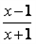 ,证明:
,证明: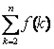 比
比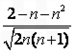 更接近0(k∈Z).
更接近0(k∈Z).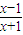 ,证明:
,证明: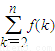 比
比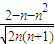 更接近0(k∈Z).
更接近0(k∈Z).