题目内容
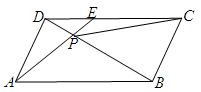
如图,在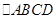 中,
中,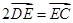 ,
,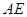 交
交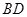 于点
于点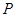 ,设
,设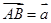 ,
,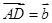 ,用
,用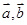 表示
表示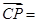 ______
______
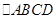 中,
中,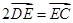 ,
,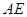 交
交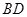 于点
于点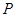 ,设
,设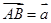 ,
,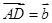 ,用
,用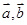 表示
表示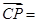 ______
______
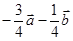
试题分析:根据题意,由于
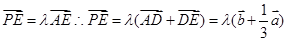 ,设
,设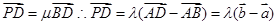 ,因为
,因为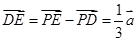 ,那么可知联立方程组得到
,那么可知联立方程组得到 ,故可知
,故可知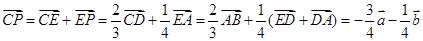 ,故答案为
,故答案为
点评:主要是考查了平面向量的基本定理的运用,熟练掌握向量的共线定理、向量的运算法则是解题的关键.属于基础题。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
题目内容
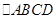 中,
中,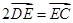 ,
,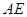 交
交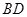 于点
于点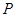 ,设
,设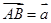 ,
,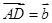 ,用
,用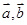 表示
表示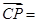 ______
______
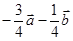
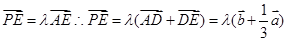 ,设
,设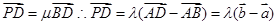 ,因为
,因为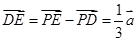 ,那么可知联立方程组得到
,那么可知联立方程组得到 ,故可知
,故可知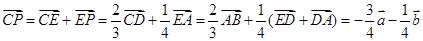 ,故答案为
,故答案为

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案