题目内容
若a,b∈R,已知直线x+a2y+1=0与(a2+1)x-2by+3=0互相垂直,则|ab|的最小值为 .
分析:根据两条直线垂直的性质求得b=
+
,再根据|ab|=|
+
|=|
|+|
|,利用基本
不等式求得它的最小值.
| 1 |
| 2 |
| 1 |
| a2 |
| a |
| 2 |
| 1 |
| a |
| a |
| 2 |
| 1 |
| a |
不等式求得它的最小值.
解答:解:由直线x+a2y+1=0与(a2+1)x-2by+3=0互相垂直,
可得 (a2+1)+a2(-2b)=-1,可得b=
+
,
∴|ab|=|
+
|=|
|+|
|≥2
=
,
当且仅当|
|=|
|时,即a=±
时,取等号,
故|ab|的最小值为
,
故答案为
.
可得 (a2+1)+a2(-2b)=-1,可得b=
| 1 |
| 2 |
| 1 |
| a2 |
∴|ab|=|
| a |
| 2 |
| 1 |
| a |
| a |
| 2 |
| 1 |
| a |
|
| 2 |
当且仅当|
| a |
| 2 |
| 1 |
| a |
| 2 |
故|ab|的最小值为
| 2 |
故答案为
| 2 |
点评:本题主要考查两条直线垂直的性质,基本不等式的应用,属于基础题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、命题:“已知函数f(x),若f(x+1)与f(x-1)均为奇函数,则f(x)为奇函数,”为直命题 | B、“x>1”是“|x|>1”的必要不充分条件 | C、若“p且q”为假命题,则p,q均为假命题 | D、命题p:”?x∈R,使得x2+x+1<0”,则?p:”?x∈R,均有x2+x+1≥0” |
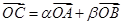 ,其中
,其中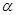
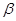 ∈R且
∈R且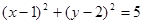 B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
B.3x+2y-11=0 C.2x-y=0 D.x+2y=5 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).