题目内容
(本小题满分12分)已知双曲线的一条渐近线方程是 ,若双曲线经过点
,若双曲线经过点 ,求此双曲线的标准方程。
,求此双曲线的标准方程。
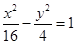 。
。
解析试题分析:根据题意,双曲线的一条渐近线方程为x-2y=0,可设双曲线方程为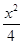 -y2=λ(λ≠0),又由双曲线过点P(4,3),将点P的坐标代入可得λ的值,进而可得答案。
-y2=λ(λ≠0),又由双曲线过点P(4,3),将点P的坐标代入可得λ的值,进而可得答案。
设双曲线的标准方程为 或
或 ;
;
∵渐近线方程为 ,即
,即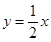 ,
,
∴当焦点在x轴上时,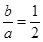 ,
,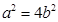 ,
,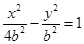 ,代入点
,代入点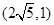 ,得
,得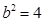 ,
,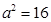
当焦点在y轴上时,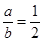 ,
, ,
,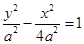 ,代入
,代入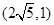 ,无解;
,无解;
∴双曲线的标准方程为: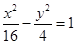 。
。
考点:本题主要考查双曲线的标准方程的求法,需要学生熟练掌握已知渐近线方程时,如何设出双曲线的标准方程.
点评:解决该试题的关键是能很熟练的运用双曲线的渐近线方程设出其双曲线的标准方程,进而利用点的坐标得到结论。

练习册系列答案
相关题目
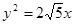 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点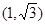 ,又知直线
,又知直线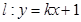 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.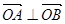 ,求实数k值.
,求实数k值. :
: (
( )的短轴长与焦距相等,且过定点
)的短轴长与焦距相等,且过定点 ,倾斜角为
,倾斜角为 的直线
的直线 交椭圆
交椭圆 、
、 两点.
两点. 轴上截距的范围.
轴上截距的范围. ,点
,点 在椭圆上。
在椭圆上。 ,直线
,直线 与椭圆交于A、B,且线段AB以M(1,1)为中点,求直线
与椭圆交于A、B,且线段AB以M(1,1)为中点,求直线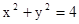 上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线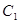 、抛物线
、抛物线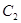 的焦点是直线y=x-1与x轴的交点.
的焦点是直线y=x-1与x轴的交点.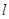 满足条件:① 过
满足条件:① 过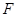 ;②与
;②与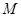 ,
,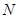 ,且满足
,且满足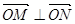 ?若存在,求出直线
?若存在,求出直线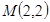 作直线
作直线 交双曲线
交双曲线 于
于 、
、 两点,且
两点,且 为
为 中点.
中点. 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.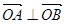 ,求实数k值.
,求实数k值. (a>b>0)的离心率
(a>b>0)的离心率 ,过点
,过点 和
和 的直线与原点的距离为
的直线与原点的距离为 .
.
 ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两 点.问:是否存在
两 点.问:是否存在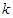 的值,
的值, 为直径的圆过
为直径的圆过 点?请说明理由.
点?请说明理由. 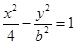 的右焦点与抛物线
的右焦点与抛物线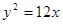 的焦点重合,求该双曲线的焦点到其渐近线的距离.
的焦点重合,求该双曲线的焦点到其渐近线的距离.